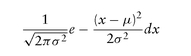Interest Rate Swaps and Their Derivatives: A Practitioner's Guide

CHAPTER 6

Black′s World

The Black-Scholes-Merton formula, and its Black variant for futures was historically derived for non-interest-rate-related underlying assets (equities, FX, commodities), and under the assumption that interest rates are nonrandom. When interest rate options (cap/floors, swaptions) were introduced, traders co-opted these formulas and applied them to interest rates. While everyone recognized that the formulae need to be adjusted since interest rates are not traded assets, and are random, nevertheless, in the absence of any other simple alternatives, Black′s formula became (and still continues to be) the standard option pricing formula for interest-rate flow products.

Therefore, we will suspend disbelief for a while and derive the Black-Scholes-Merton formula in a world where interest rates are deterministic, and then turn around and apply these to interest rate options!

Before we get there, however, a bit of probability review is in order.

A LITTLE BIT OF RANDOMNESS

A random variable (r.v.) X is said to have a Normal distribution with mean µ and standard deviation σ , if the probability that it lies in some region [x, x + dx] is approximately

We will use the shorthand X ~ N(µ, σ ² ). More precisely, the cumulative distribution function (CDF) of an N(µ, σ ² ) random variable X is

FIGURE 6.1 Distribution Function of a Normal N(µ, σ ²) Random Variable