Numerical Methods for Engineers and Scientists 3rd Edition

Chapter 1

Introduction

Core Topics

Representation of numbers on a computer (1.2).

Errors in numerical solutions, round-off errors and truncation errors (1.3).

Computers and programming (1.4).

1.1 BACKGROUND

Numerical methods are mathematical techniques used for solving mathematical problems that cannot be solved or are difficult to solve analytically. An analytical solution is an exact answer in the form of a mathematical expression in terms of the variables associated with the problem that is being solved. A numerical solution is an approximate numerical value (a number) for the solution. Although numerical solutions are an approximation, they can be very accurate. In many numerical methods, the calculations are executed in an iterative manner until a desired accuracy is achieved.

For example, Fig. 1-1 shows a block of mass m being pulled by a force F applied at an angle θ. By applying equations of equilibrium, the relationship between the force and the angle is given by:

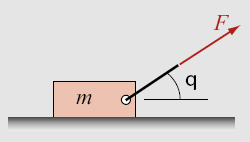
Figure 1-1: Motion of a block on a surface with friction.

where µ is the friction coefficient and g is the acceleration due to gravity. For a given value of F, the angle that is required for moving the block can be determined by solving Eq. (1.1) for θ. Equation (1.1), however, cannot be solved analytically for ...