Chapter 29. The Relationship of 4D Rotations to Quaternions
What Happened in Three Dimensions
In three dimensions, there were many ways to deduce the quadratic mapping from quaternions to the 3 × 3 rotation matrix belonging to the group SO(3) and implementing a rotation on ordinary 3D frames. The one most directly derived from the quaternion algebra conjugates “pure” quaternion three-vectors vi = (0, Vi) and pulls out the elements of the rotation matrix in the following way:
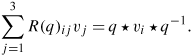
We easily find that the quadratic relationship between R3(q) and q = (q0, q1, q2, q3) is
Equation 29.1.
Quaternions and Four Dimensions
In the 4D case, which we should really regard ...
Get The Morgan Kaufmann Series in Interactive 3D Technology: Visualizing Quaternions now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

