
30 Applied calculus of variations for engineers
First we separate the variables
dy = ±
x − c
1
λ
2
− (x − c
1
)
2
dx,
and integrate again to produce
y(x)=±
λ
2
− (x − c
1
)
2
+ c
2
.
It is easy to reorder this into
(x − c
1
)
2
+(y − c
2
)
2
= λ
2
,
which is the equation of a circle. Since the two given points are on the x axis,
the center of the circle must lie on the perpendicular bisector of the chord,
which implies that
c
1
=
x
0
+ x
1
2
.
To solve for the value of the Lagrange multiplier and the other constant, we
consider that the circular arc between the two points is the given length:
L = λθ,
where θ is the angle of the arc. The angle is related to the remaining constant
as
2Π − θ = atan(
x
1
− x
0
2c
2
).
The two equations may be simultaneously satisfied with
θ =Π,
resulting in the shape being a semi-circle. This yields the solutions of
c
2
=0
and
λ =
L
π
.
The final solution function in implicit form is
(x −
x
0
+ x
1
2
)
2
+ y
2
=(
L
π
)
2
,
or explicitly
y(x)=
(
L
π
)
2
− (x −
x
0
+ x
1
2
)
2
.
Constrained variational problems 31
0
0
.1
0
.2
0
.3
0
.4
0
.5
0
.6
0
.7
0 0.2 0.4 0.6 0.8 1
g(x)
y(x)
’_’
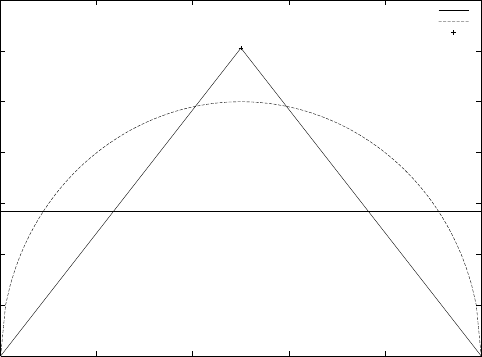
FIGURE 2.1 Maximum area under curves
It is simple to verify that the solution produces the extremum of the original
variational problem.
Figure 2.1 visibly demonstrates the phenomenon with three curves of equal
length (π/2) over the same interval. None of the solid curves denoted by
g(x), the triangle, or the rectangle cover as much area as the semi-circle y(x)
marked by the dashed lines.
2.3.2 Optimal shape of curve of given length under gravity
Another constrained variational problem, whose final result is often used in
engineering, is the rope hanging under its weight. The practical importance of
the problem regarding power lines and suspended cables is well-known. Here
we derive the solution of this problem from a variational origin.
A body in a force field is in static equilibrium when its potential energy has
a stationary value. Furthermore, if the stationary value is a minimum, then
the body is in stable equilibrium. This is also known as principle of minimum
potential energy.
32 Applied calculus of variations for engineers
Assume a body of a homogeneous cable with a given weight per unit length
of ρ = constant, and suspension point locations of
P
0
=(x
0
,y
0
),
and
P
1
=(x
1
,y
1
).
These constitute the boundary conditions. A constraint is also given on the
length of the curve: L. The potential energy of the cable is
E
p
=
P
1
P
0
ρyds
where y is the height of the infinitesimal arc segment above the horizontal
base line and ρds is its weight. Using the arc length formula we obtain
E
p
= ρ
x
1
x
0
y
1+y
2
dx.
The principle of minimal potential energy dictates that the equilibrium posi-
tion of the cable is the solution of the variational problem of
I(y)=ρ
x
1
x
0
y
1+y
2
dx = extremum,
under boundary conditions
y(x
0
)=y
0
; y(x
1
)=y
1
and constraint of
x
1
x
0
1+y
2
dx = L.
Introducing the Lagrange multiplier and the constrained function
h(y)=ρy
1+y
2
+ λ
1+y
2
,
the Euler-Lagrange differential equation of the problem after the appropriate
differentiations becomes
ρ
1+y
2
−
d
dx
(ρy + λ)y
1+y
2
=0.
Some algebraic activity, which does not add anything to the discussion, and
hence is not detailed, yields
(ρy + λ)(
y
2
1+y
2
−
1+y
2
)=c
1
,

Constrained variational problems 33
where the right-hand side is a constant of the integration. Another integration
results in the solution of the so-called catenary curve
y = −
λ
ρ
−
c
1
ρ
cosh(
ρ(x − c
2
)
c
1
),
with c
2
being another constant of integration. The constants of integration
may be determined by the boundary conditions albeit the calculation, due to
the presence of the hyperbolic function, is rather tedious. Let us consider the
specific case of the suspension points being at the same height and symmetric
with respect to the origin. This is a typical engineering scenario for the span
of suspension cables. This results in the following boundary conditions:
P
0
=(x
0
,y
0
)=(−s, h)
and
P
1
=(x
1
,y
1
)=(s, h).
Without the loss of the generality, we can consider unit weight (ρ =1)and
by substituting above boundary conditions we obtain
h + λ = c
1
cosh(
−s + c
2
c
1
)=c
1
cosh(
s + c
2
c
1
).
This implies that
c
2
=0.
The value of the second coefficient is solved by adhering to the length con-
straint. Integrating the constraint equation yields
L =2c
1
sinh(
s
c
1
)
whose only unknown is the integration constant c
1
. This problem is not solv-
able by analytic means; however, it can be solved by an iterative procedure
numerically by considering the unknown coefficient as a variable:
c
1
= x,
and intersecting the curve
y = xsinh(
s
x
)
and the horizontal line
y =
L
2
.
The minimal cable length must exceed the width of the span, hence we
expect the cable to have some slack. Then, for example, using
L =3s
Get Applied Calculus of Variations for Engineers, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

