Kalman Filter see Filtering
Kelly Problem
Consider a financial market with K assets whose prices Pi(t), i = 1, …, K are stochastic, dynamic processes, and a risk-free asset whose price is P0(t). The vector of prices at time t is
If the prices are given at points in time t1 and t2, with t1 < t2, then the rate of return over that time on a unit of capital invested in asset i is
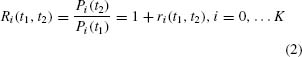
When there are dividends Di accrued in the time interval, then the return is Ri(t1, t2) = (Pi(t2) + Di(t2 − t1))/Pi(t1).
Suppose an investor has wt units of capital at time t, and that capital is fully invested in the assets, with the proportions invested in each asset given by xi(t), i = 0, … K, where 
. Then an investment or trading strategy at time t is the vector process
Given the investments wt1 X(t1) at time t1, the accumulated capital at time t2 is
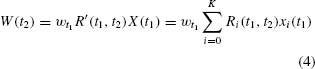
The trajectory of returns between time t1 and time t2 depends ...
Get Encyclopedia of Quantitative Finance, IV Volume Set now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
