Encyclopedia of Quantitative Finance, IV Volume Set

TABX see ABS Indices

Tanaka Formula see Local Times

Targeted Accrual Redemption Note (TARN), TARN see Trigger Swaps

Tempered Stable Process

A tempered stable process is a pure-jump Levy process (see Lévy Processes) with infinite activity (see Exponential Lévy Models) whose small jumps behave like a stable process, while the large jumps are “tempered” so that the tail of the density decays exponentially. Tempered stable processes can be constructed from stable processes by exponential tilting (see Esscher Transform) of the Levy measure.

Tempered stable processes were introduced in [8] and introduced in financial modeling by Cont et al. [4] under the name truncated stable process, where it was noted that tempered stable processes have a short-time behavior similar to stable Levy processes while retaining finite variance and finite exponential moments. Option pricing with tempered stable processes was studied in [1], [2], and [5].

The best known example of tempered stable processes is the CGMY process introduced in [2], which is a pure-jump Levy process with Levy density given by

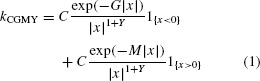
The model parameters of equation (1) fulfill C > 0, G, M ≥ 0, and Y (−∞, 2). The restriction on the parameter ...