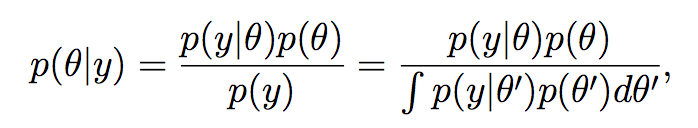Bayes theorem states the following:
Posterior = Prior * Likelihood
This can also be stated as P (A | B) = (P (B | A) * P(A)) / P(B) , where P(A|B) is the probability of A given B, also called posterior.
Prior: Probability distribution representing knowledge or uncertainty of a data object prior or before observing it
Posterior: Conditional probability distribution representing what parameters are likely after observing the data object
Likelihood: The probability of falling under a specific category or class.
This is represented as follows: