Mathematik

B Lösungen

Aufgabe 1:

„∀a∀b : a + b = b + a“ wird gelesen als „für alle a und alle b gilt, dass a + b gleich b + a ist“.

„∀a∃!b : ab = 1“ ist entsprechend „für alle a gibt es genau ein b, so dass gilt: a mal b ist gleich 1“.

„∀a : ist_gerade(a) lässt keinen Rest“ lasst sich als „für alle a gilt: a istgenau dann gerade, wenn die Division von a durch 2 keinen Rest lässt“ lesen.

Aufgabe 2:

Induktionsanfang: Für n = 1 gilt offensichtlich

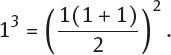
Induktionsschritt: Zu zeigen ist, dass die Aussage aus Gleichung (1.5) unter der Annahme, dass sie für n gilt, ...