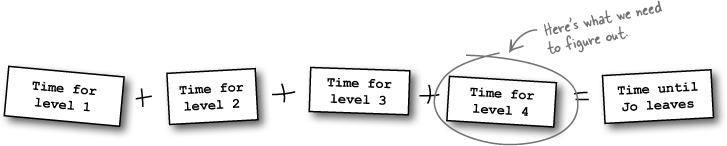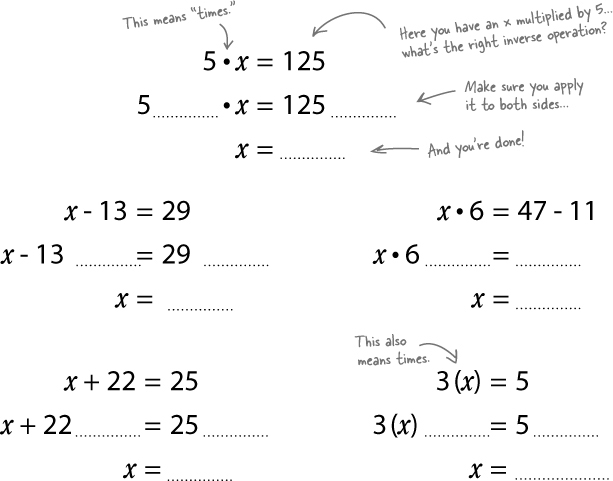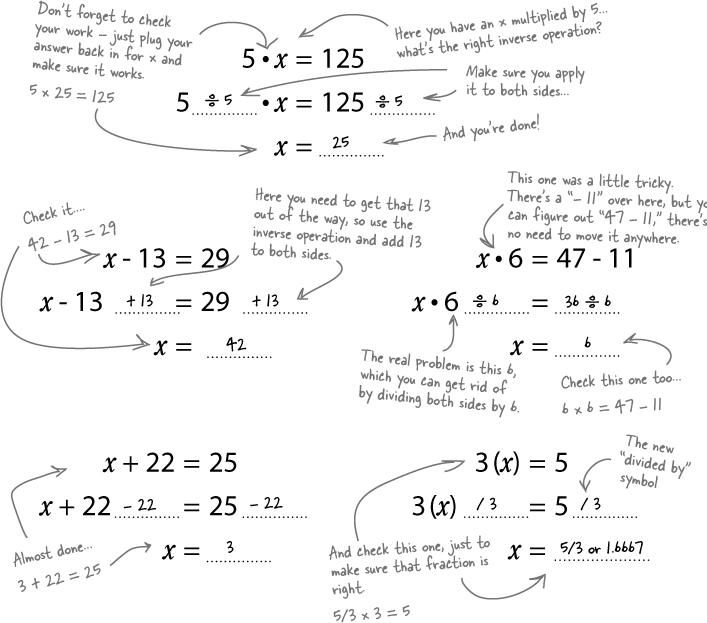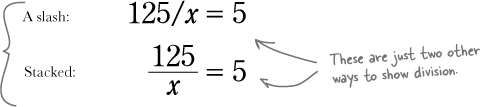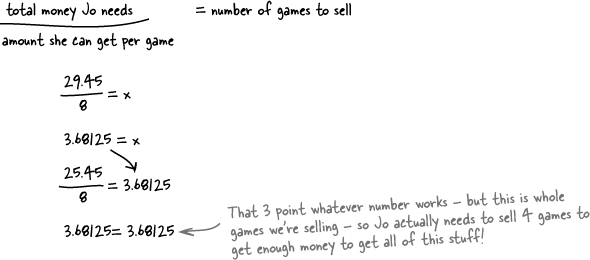Head First Algebra

Chapter 1. What is Algebra?: Solving for unknowns...

Do you ever wish you knew more than know? Well, that’s what Algebra’s all about: making unknowns known. By the time you’re through this first chapter, you’ll already have a handle on X being a lot more than a mark where treasure’s buried. You’ll get a handle on equations, keeping both sides of an equation balanced, and why solving for unknowns really isn’t that big of a deal. What are you waiting for? Go on and get started!

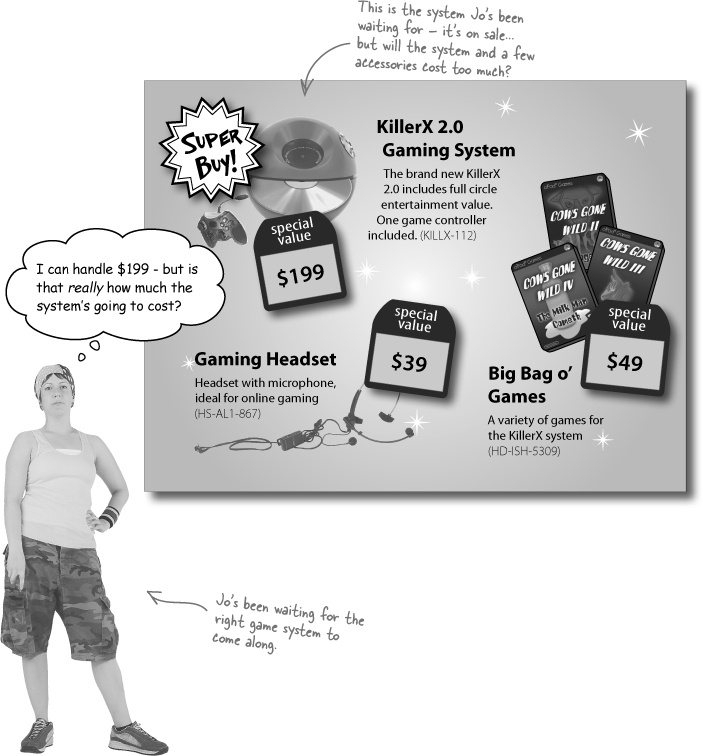
It all started with a big gaming sale

Jo has been watching the game system battles for a while now and has finally decided on the one she wants. Her favorite system’s on sale this week, and she’s ready to buy. But can she afford it? That’s where she needs a little help from you.

What does a system really cost?

When you buy things—especially expensive electronic things—there are lots of pieces that add into the price besides just the number on a sales flyer: sales tax, an extended warranty, shipping and handling, etc. So what will a KillerX system really cost?

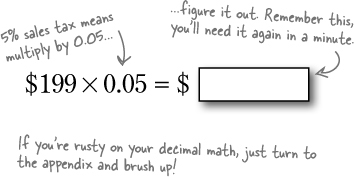
There’s tax on the system...

The base price of the system is $199. After that, we need to think about taxes, which are 5%. Let’s figure out how much Jo’ll have to pay in taxes:

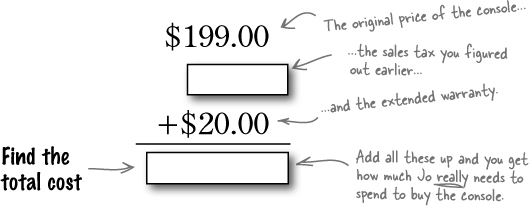
... and the extended warranty, too.

Jo’s about to spend $199 on a game machine, and she wants to purchase an extended warranty plan for an additional $20. Let’s put that in the price, too. What price will Jo need to pay?

Figuring out the total wasn’t just addition! It was solving for an unknown—and that’s Algebra. In this case the unknown was how much everything was going to cost.

Algebra is about solving for unknowns

Algebra is about finding the missing information that you’re looking for by using the information you already have. The unknown could be the cost of a car loan, the quantity of soda you need, or how high you can throw a water balloon. If you don’t know it, it’s an unknown.

All the other things that you’ll learn in Algebra are just ways to jiggle things around to help you find a piece of missing information. There are rules about when you can multiply things or when you can bump something from one side of an equals sign to another, but at the end of the day, they’re all just tricks to help you find that missing piece of information you’re looking for.

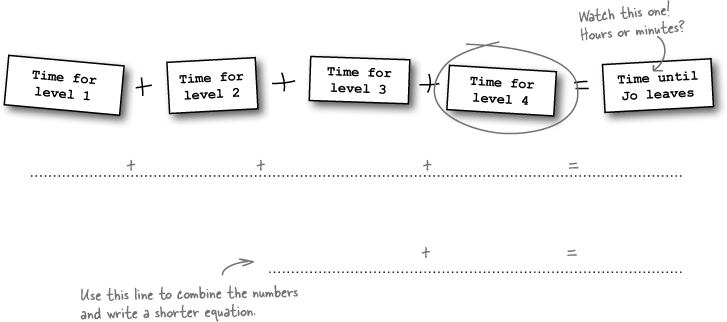
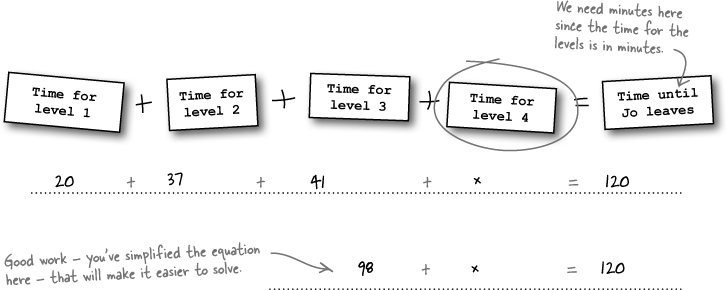
Jo’s got more unknowns

So Jo knows how much it will take to buy an awesome gaming system, including an extended warranty. But she still doesn’t have any games... or another controller... or a headset.

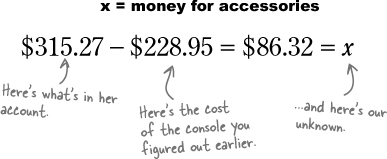
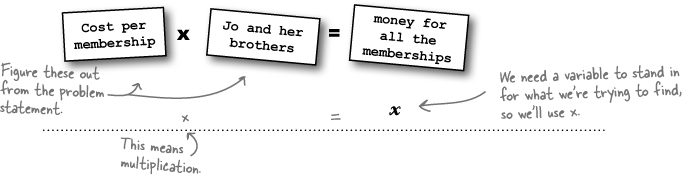
Jo started with $315.27 in her bank account. Now that she’s paid for the console, how much can Jo spend on accessories? Let’s start by writing this out in words:

We know how much the console costs ($228.95), and we know how much Jo has in her account ($315.27). Now just fill in the blanks, and we can figure out Jo’s accessory budget:

Console Pricing Up Close

Let’s take a closer look at what we just did. First, we’re going to swap out the unknown box for the standard Algebra version of an unknown—an x.

Note

There’s no magic to the letter x - that’s just the most common letter used in Algebra.

Understanding a problem and finding the unknown, x, is working with Algebra. Using tricks like writing the problem out with words and flipping things around are just ways to make finding that unknown possible.

Solving for any unknown is Algebra.

X marks the spot unknown

x is just a user-friendly stand-in for the unknown box we used earlier. x is easier to write and it’s what you’re looking for when you solve an equation. The unknown in any given situation is called a variable. In the real world, problems present themselves every day; translating them into mathematical equations allows you to solve them.

There are no Dumb Questions

Q:	Q: Will the unknown always be x?
A:	A: Nope. As you progress with math, you’ll see x, y, and z pretty often. You can use any letter that you want, though.
Q:	Q: Back in Console Pricing Up Close, how come you could just flip that equation?
A:	A: All we really did was switch the same equation around, called manipulating the equation. There are rules about exactly how you can work with equations without changing any values, and we’ll learn lots more about them in the rest of this book.

Equations are math sentences

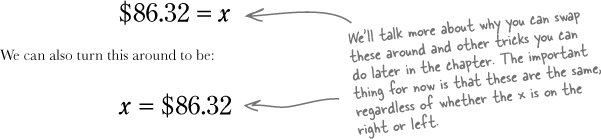
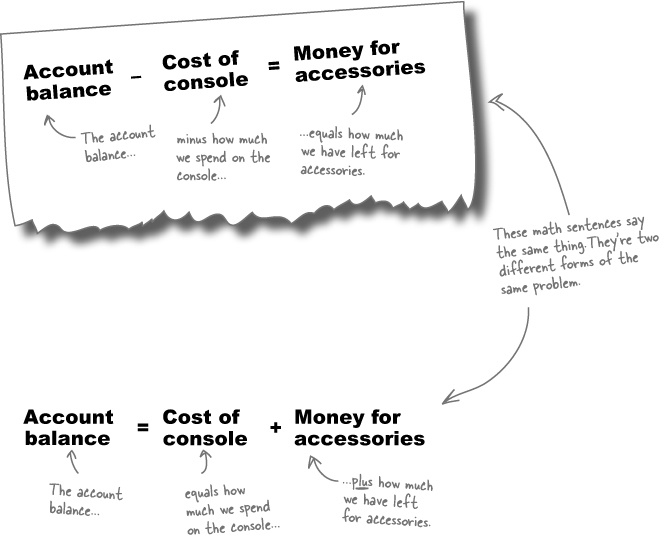
Equations, like the one you used earlier to figure out how much Jo could spend on accessories, are just math sentences. They’re a mathematical way of saying something. So when we talked about Jo’s account balance, we were actually using an equation:

Our equation means “The account balance minus how much we spend on the console equals how much we have left for accessories.” So, that means that the account balance must equal the cost of the console plus the money for accessories. If we write that sentence as an equation it looks like this:

Equations can be rearranged like sentences.

Both sentences mean the same thing; they’re just phrased differently. Over the next few pages, you’ll learn how to rearrange math sentences and make sure that you don’t change any values.

Math Magnets

Below are some word problems and magnets. Your job is to make equations from the magnets that say the same thing as the word problems. Once you have the equation put together, circle the unknown—the value you need to figure out. Then, write out your equation in a complete phrase.

1. Jo and her 3 brothers are thinking about upgrading their LIVE subscription to the Platinum membership, which is $12 per person. How much will it cost them in total?

2. Jo started playing a hot new game, but she only has two hours before she has to go out. She spent 20 minutes on level 1, 37 minutes on level 2, and 41 minutes on level 3. How much time does she have left to play level 4?

Note

This time you build the whole equation...

Now write your equation in words:

_____________________________________________________________________

_____________________________________________________________________

Math Magnets Solutions

Below are some word problems and magnets. Your job is to make equations from the magnets that say the same thing as the word problems. Once you have the equation put together, circle the unknown—the value you need to figure out. Then, write out your equation in a complete phrase.

1. Jo and her 3 brothers are thinking about upgrading their LIVE subscription to the Platinum membership, which is $12 per person. How much will it cost them in total?

2. Jo started playing a hot new game, but she only has two hours before she has to go out. She spent 20 minutes on level 1, 37 minutes on level 2, and 41 minutes on level 3. How much time does she have left for level 4?

Brain Power

You could also have made an equation that says, “Time until Jo leaves minus the time for level 1 minus the time for level 2 minus the time for level 3 equals the time for level 4.” Would that be any better? Why?

Equation Construction

Now you build the equations! Take the “math sentence” you wrote and translate it into an equation. Use the numbers that were given and x for the unknown.

1. Jo and her 3 brothers are thinking about upgrading their LIVE subscription to the Platinum membership, which is $12 per person. How much will it cost them in total?

Note

The same thing for this problem - you fill in the x for the unknown.

2. Jo started playing a game that just came out, but she only has two hours before she has to go out. She spent 20 minutes on level 1, 37 minutes on level 2, and 41 minutes on level 3. How much time does she have left for level 4?

Equation Construction Solution

Now you can build the equations! Take the “math sentence” you wrote and translate it into an Algebraic equation. Use the numbers that were given and x for the unknown.

1. Jo and her 3 brothers are thinking about upgrading their LIVE subscription to the Platinum membership, which is $12 per person. How much will it cost them in total?

2. Jo started playing a game that just came out - but she only has two hours before she has to go out. She spent 20 minutes on level 1, 37 minutes on level 2, and 41 minutes on level 3. How much time does she have left for level 4?

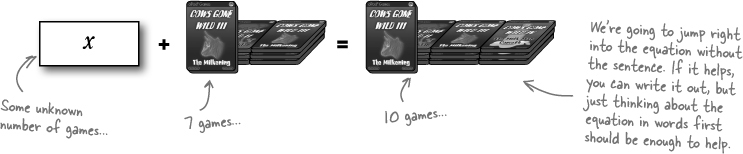
Now SOLVE for the unknown

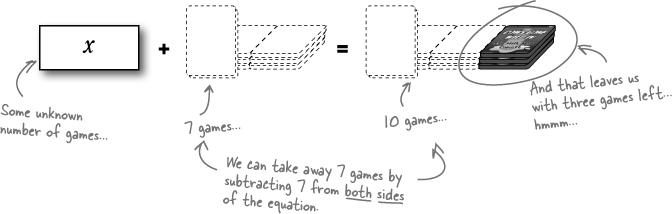
Jo is trying to decide if it’s worth it for her to buy a LIVE subscription. She has 10 games, and 7 of them don’t have any online play. How many does she have that can be played online? Does it make sense for her to buy the subscription?

What we really care about here is what x is—the unknown number of games. We don’t really care about the seven games on the left side of the equation. In fact, we can get rid of that seven as long as we make sure we do the same thing to both sides of the equation.

An equals sign means that both sides are the same. So if we take 7 away from one side, we have to do the same thing to the other side of the equation:.

So here’s what we have left:

You don’t need pictures to do algebra.

What you need is a way to use the operations that you already know (addition, subtraction, multiplication, and division) to solve equations.

The tricky part? You must preserve the equality. Equality means the same. When you do something to one side of the equation, you have to do the same thing to the other side of the equation.

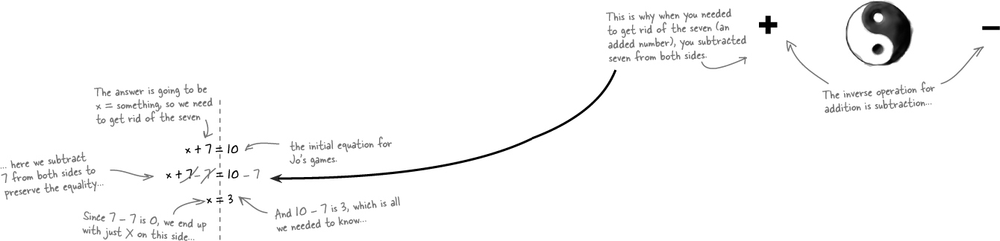
Here’s another way to look at Jo’s online problem without pictures:

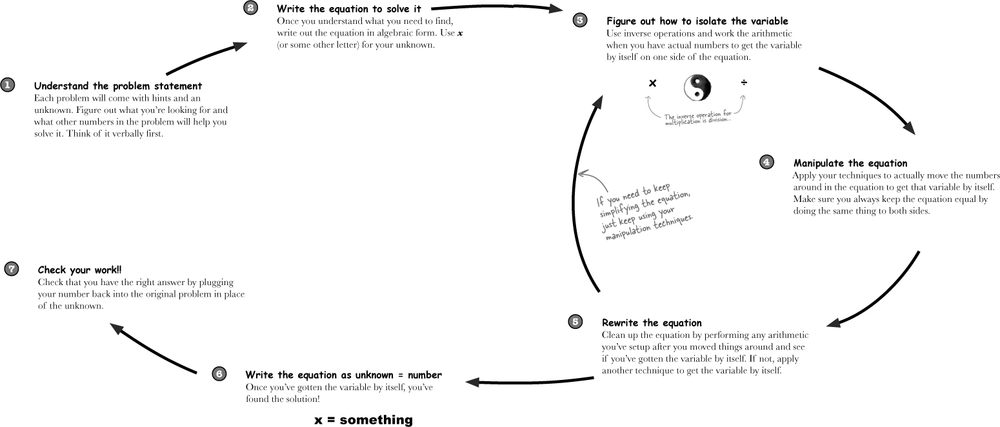
When you get x all by itself, you’re isolating the variable. That’s the most important part of solving an equation. Isolating the variable means you’ve gotten the variable by itself on the left side of the equation and everything else stacked up over on the right. If you can isolate a variable, then you’ve solved the equation—the answer just pops out, like x = 3.

Knowing that your goal is to isolate the variable means that you know which numbers to move away from the left side. Since you’re trying to get x alone, that means that you move the seven, not the 10!

So which operation do you use when?

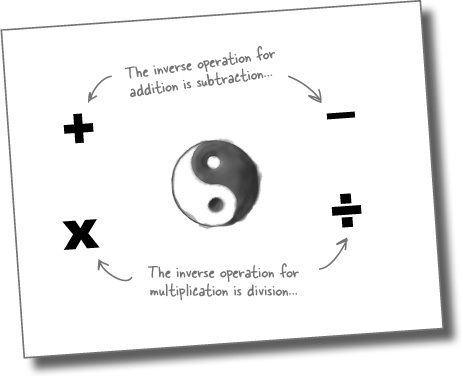
The opposite of addition is subtraction. So, if some number is being added on one side of the equation, and you want to move that number to the other side, you can subtract that number from both sides. The math term that describes opposite operations is inverse operations.

The basic math operations are addition, subtraction, multiplication, and division. An inverse operation is the operation that undoes an operation (like addition undoes subtraction). Inverse operations let you shift a number or variable from one side of the equation to the other by “undoing” that number on one side of an equation.

When you want to solve an equation:

1. Look at the equation and figure out what numbers to move.

   Using Jo’s equation, we had to get rid of the 7. That’s because we’re trying to isolate the variable, the x.

2. Figure out which operation to use.

   You need to use the inverse operation for the number to remove it. For a subtracted number, add. For a divided number, multiply, and so on.

3. Preserve equality.

   Whatever you decide to do to one side of the equation, you must do to the other. That keeps the equation the same.

Brain Power

There are other inverse operations out there. Can you think of other operation pairs that work?

Inverse Operations Exposed

This week’s interview: Just who are the inverse operations?

Head First: And welcome back to Algebra at Night. Tonight’s guest... or guests... are inverse operations. So do you guys always travel in pairs?

Inverse Ops: Well, yes. We’re not inverse operations unless both of us are here. We’re about maintaining balance.

Head First: Ah, right. So addition is always paired with subtraction, multiplication always with division.. why is that?

Inverse Ops: Opposites attract, and multiplication is the opposite of division.

Head First: Same with addition and subtraction, right?

Inverse Ops: Yeah, and we’re all opposites because we all undo each other.

Head First: When you say undo each other, do you mean if there’s a multiplication, than division can make it go away?

Inverse Ops: Well, not really go away—remember, our job is to keep everything in balance. We just move things around. If you have a multiplication you need to move, you can undo that multiplication with a division—on both sides of the equation.

Head First: Ok, I think I get it—you can move numbers from one side of the equation to the other. So you’re pretty useful for getting a variable by itself?

Inverse Ops: Absolutely! That’s what we do best. A little addition here or multiplication there, and you can get almost any variable by itself.

Head First: Very cool! So any last words before we sign off?

Inverse Ops: Just a couple thoughts. You have to be careful that you keep the equation balanced. There are also a few more pairs of us floating around out there, but they’ll turn up later.

Head First: Well, it’s been great talking to you—all of you—and I appreciate you coming by. Until next time, may your multiplications always have a division, and your additions subtract.

Inverse operations help you isolate the variable.

Bullet Points

• Algebra is about solving for unknowns.

• You use other information from your problem to setup an equation with the unknown.

• The unknown is called a variable.

• In order to solve for a variable (like x), you need to isolate the variable.

• You can isolate the variable by using inverse operations to manipulate the equation.

• Addition is the inverse of subtraction, and multiplication is the inverse of division.

Sharpen your pencil

Below are equations that have unknowns and numbers on both sides of the equations. Use inverse operations to isolate the variable and solve the equation.

Whoever thought it was a good idea to use x to mean the typical unknown apparently didn’t mind the confusion it might cause with the multiplication sign, x. However, lots of other people did.

They gave up on using x for multiplication and came up on with a few easier to read options:

Sharpen your pencil Solution

Below are equations that have unknowns and numbers on both sides of the equations. Your job was to use inverse operations to isolate the variable and solve the equation.

And a change for division too...

The division sign you’re used to seeing was tossed away, too. Instead you’ll see things like this:

Who Does What?

Match each example of something you’ve learned in this chapter to it’s name. Be careful, some of the names are used twice!

Operation example	Operation name
Inverse operation for addition	Division
Opposite of multiplication	Equation
7/3 x	Manipulating the equation
2x = 10	Variable
x · 3 _______ = 5 _______	Subtraction

Who Does What? Solution

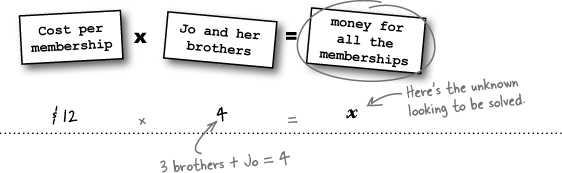
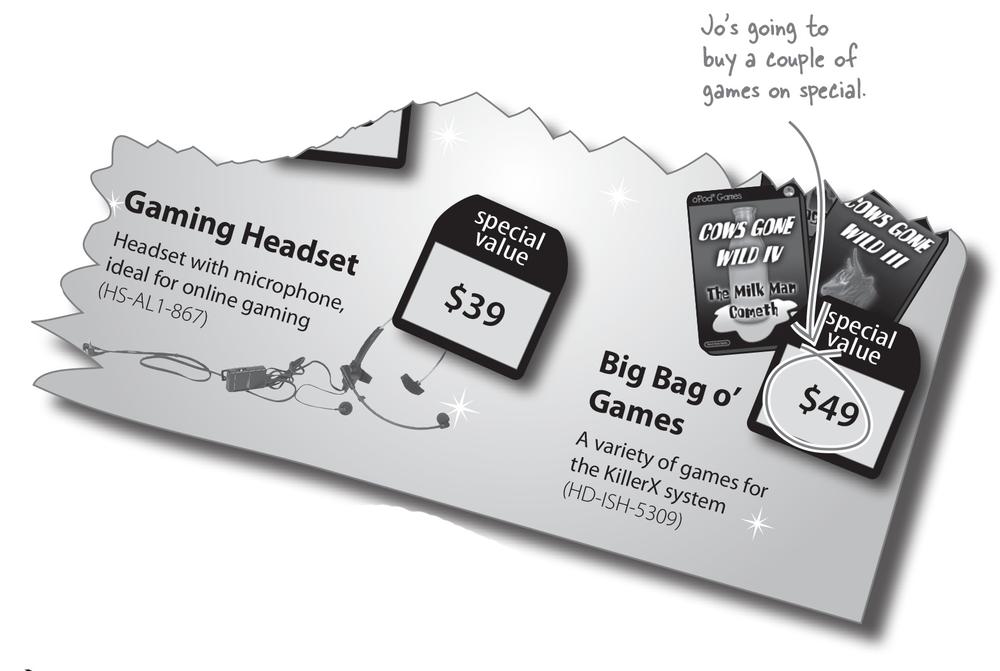
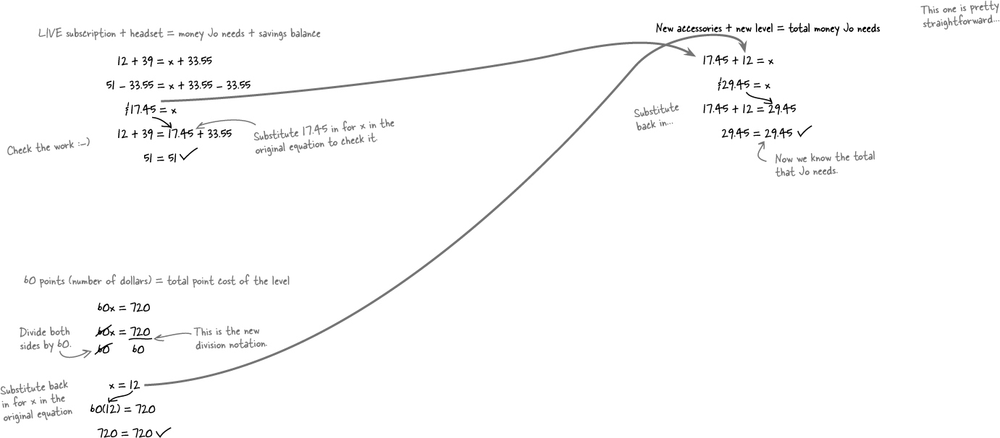
Jo is ready to accessorize!

Jo figured out that she had $86.32 left in her account for accessories. She decided that she wants to get more games and not worry about the headset just yet.

Jo did some quick Algebra to figure out how many games she can buy:

Sharpen your pencil

Fix Jo’s problem! Figure out where she went wrong.

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

Sharpen your pencil Solution

Fix Jo’s problem! Figure out where Jo went wrong.

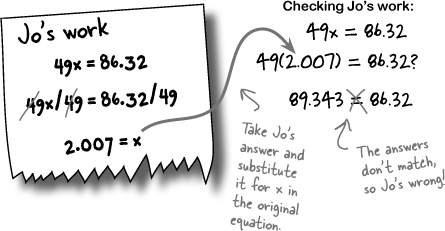
Cecking Checking your work...

You’ll find as you go forward with Algebra that the problems become more complicated, and it’s pretty easy to make a mistake. Jo didn’t divide correctly, and that got her! Checking your work doesn’t mean just looking over what you did. It also means using a specific technique called substitution.

Substitution uses your solution in the original equation

Substitution means putting something in for something else. A substitute teacher is in the place of a regular teacher, right? To check your work, you substitute in the answer you found for the variable in the original equation.

Substitution is a process that can be used not just for checking your work, but for other things too. When we get to more complex equations, and equations with more than one variable, you’ll want to use substitution as part of the solving process.

There are no Dumb Questions

Q:	Q: So about this “checking your work” thing...
A:	A: Do it. It’s easy to do, and it will tell you if you have the right answer!! Seriously. If you have an equation like 5 + x = 11, and you say x = 2, when you plug 2 back in you end up with 5 + 2 = 11, which is seriously wrong. x does not equal 2. It’s easy to check your work after you’ve solved for the unknown.
Q:	Q: When else will we use substitution?
A:	A: You’ll see it come up again and again—always with checking your work, but also as a starting point to solve equations with two variables, for graphing lines, figuring out inequalities ...keep reading, we’re getting there!
Q:	Q: Why are there different notations for multiplication and division?
A:	A: It’s really more convenient and a lot less confusing than the traditional multiplication and division signs. As you get to later chapters, you’ll see more complicated equations where being able to show division as a single line really makes a huge difference. Multiplication (especially with parentheses) is the same way—sometimes what’s inside that parentheses can get pretty complicated. Finally, multiplying a number by a variable is so common that just writing them next to each other is a lot less confusing than having a multiplication symbol in between.
Q:	Q: When should I use parentheses versus dots versus just bumping the number and variable together?
A:	A: There’s no difference between the different notations; it’s just whatever is easier and looks cleanest. If you have a number times a bunch of things, you can use parentheses. We’ll talk a lot more about that in Chapter 2. If you have a number times a variable, just push them together. As for the dot... well, it’s good for variety if you’re bored with the other notations. With division, you almost always see the stacked form, unless you’re typing an equation in a word processor or an email, where the stacked form is a pain. In those cases, you can use the slash.
Q:	Q: Do addition and subtraction have other notations, too?
A:	A: Nope, they stay the same. Plus means addition, and the minus means subtraction, but...
Q:	Q: What’s the difference between a negative number and subtracting a positive number?
A:	A: As far as working with them, none. That means that when you have a -4, it’s the same thing as + (- 4).
Q:	Q: There seem to be a lot of elements that go into solving an equation, how do I keep track?
A:	A: There are a lot, but they’ll soon become second nature. Once you get used to working with equations, you’ll automatically use inverse operations to move numbers around, you’ll simplify the equation you end up with, and then you’ll just keep going until you get that variable by itself. Later we’ll follow the exact steps, but really they are just “what you do” when you get an equation. Probably the easiest one to forget is checking your work...make sure you do it!

Substitution means putting a new value back into the original equation.

Exercise

Jo’s perfecting her set up with that new game she bought with what she had left of her savings. Help her figure out the details!

During Jo’s embarrassing trip the first time she tried to buy the games, she put back the headset and just bought the new game, so she has $33.55 left. The new game is networked, so it’s time to invest in that LIVE subscription ($12) and the headset ($39). How much does she need to save up to buy all of these accessories?

Note

Make sure to check your work...

Jo wants to buy an extra level for her game on LIVE, and it’s 720 points. It costs $1 for 60 points. How much will it cost for the new level?

Now how much does Jo need to come up with? She wants all the accessories and the new level for her game...

Jo has figured out that she can sell some used games that she’s already beaten to pay for the headset, subscription, and extra level. She can get $8 a game. How many games does she need to sell to cover the new stuff?

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

Exercise Solution

Jo’s perfecting her set up with that new game she bought with what she had left of her savings. Help her figure out the details!

During Jo’s embarrassing trip the first time she tried to buy the games, she put back the headset and just bought the new game, so she has $33.55 left. The new game is networked, so it’s time to invest in that LIVE subscription ($12) and the headset ($39). How much does she need to save up to buy all of these accessories?

Jo wants to buy an extra level for her game on LIVE, and it’s 720 points. It costs $1 for 60 points. How much will it cost for the new level?

Now how much does Jo need to come up with? She wants all the accessories and the new level for the game...

Jo has figured out that she can sell some used games that she’s already beaten to pay for the headset, subscription, and extra level. She can get $8 a game. How many does she need to sell to cover the new stuff?

Equation training

Let’s put all your mad equation solving skills together to solve a real world problem using Algebra:

Jo has an awesome setup!

After a trip to sell off 4 games and buy a headset, Jo signed into LIVE and bought that new level, and she is ready to play!

Jo’s about to spend hours on her new game—but when she’s done, it’ll be easy to figure out what game she can afford next!

Equationcross

Take some time to sit back and give your right brain something to do. It’s your standard crossword; all of the solution words are from this chapter.

Across	Down
2. The operation that undoes some other operation. 5. Use this to do away with addition. 6. Checking your work is really just .......... 8. Plug your answer back in to .......... it. 10. A variable, by itself. 11. Jiggling the equation around to solve it.	1. The anti-multiplication. 3. Stands for an unknown. 4. Math sentences. 7. Algebra is solving for .......... 9. The key thing an equation promises.

Math Toolbox

Bullet Points

• Algebra is about solving for unknowns.

• You use other information from your problem to setup an equation with the unknown.

• The unknown is called a variable.

• In order to find the solution to the equation, you need to isolate the variable.

• You can isolate the variable by using inverse operations to manipulate the equation.

• Addition is the inverse of subtraction, and multiplication is the inverse of division.

Equationcross solution