Jim Blinn's Corner: Notation, Notation, Notation

Chapter Nineteen

Polynomial Discriminants Part I, Matrix Magic

November–December 2000

$\det \left[\begin{array}{cc}2\det \left[\begin{array}{cc}A& B\\ B& C\end{array}\right]& \det \left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\\ \det \left[\begin{array}{cc}A& B\\ C& D\end{array}\right]& 2\det \left[\begin{array}{cc}B& C\\ C& D\end{array}\right]\end{array}\right]$

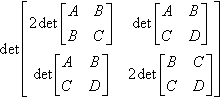
I like beautiful equations. But beauty is sometimes subtle or hidden by bad notation. In this chapter and the next, I am going to reveal some of the hidden beauty in the explicit formulation of the discriminants of polynomials. Along the way, I will drag in some clever algebra, promote some notational schemes from mathematical physics, and illustrate some ways of visualizing homogeneous space. This will ultimately lead us to some interesting ways to find roots of these polynomials, a task that will become more and more important as ...