An Introduction to Optimization, 4th Edition

CHAPTER 18

NONSIMPLEX METHODS

18.1 Introduction

In previous chapters we studied the simplex method and its variant, the revised simplex method, for solving linear programming problems. The method remains widely used in practice for solving LP problems. However, the amount of time required to compute a solution using the simplex method grows rapidly as the number of components n of the variable x ⁿ increases. Specifically, it turns out that the relationship between the required amount of time for the algorithm to find a solution and the size n of x is exponential in the worst case. An example of an LP problem for which this relationship is evident was devised by Klee and Minty in 1972 [76]. Below, we give a version of the Klee-Minty example, taken from [9]. Let n be given. Let

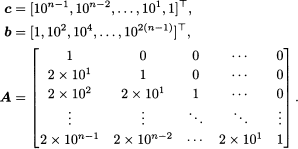
Consider the following LP problem:

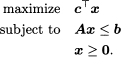
The simplex algorithm applied to the LP problem above requires 2ⁿ − 1 steps to find the solution. Clearly, in this example the relationship between the required amount of time for the simplex algorithm to find a solution and the size n of the variable x is exponential. This relationship ...