An Introduction to Optimization, 4th Edition

CHAPTER 22

CONVEX OPTIMIZATION PROBLEMS

22.1 Introduction

The optimization problems posed at the beginning of this part are, in general, very difficult to solve. The source of these difficulties may be in the objective function or the constraints. Even if the objective function is simple and “well-behaved,” the nature of the constraints may make the problem difficult to solve. We illustrate some of these difficulties in the following examples.

Example 22.1 Consider the optimization problem

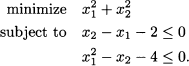
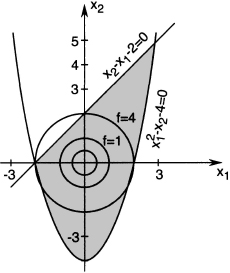
The problem is depicted in Figure 22.1, where, as we can see, the constrained minimizer is the same as the unconstrained minimizer. At the minimizer, all the constraints are inactive. If we had only known this fact, we could have approached this problem as an unconstrained optimization problem using techniques from Part II.

Figure 22.1 Situation where the constrained and the unconstrained minimizers are the same.

Example 22.2 Consider the optimization problem

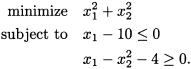
The problem is depicted in Figure 22.2. At the solution, only one constraint is active. If we had only known about this we could have handled this problem as a constrained optimization problem using the Lagrange multiplier method.

Figure ...