CHAPTER 21
PROBLEMS WITH INEQUALITY CONSTRAINTS
21.1 Karush-Kuhn-Tucker Condition
In Chapter 20 we analyzed constrained optimization problems involving only equality constraints. In this chapter we discuss extremum problems that also involve inequality constraints. The treatment in this chapter parallels that of Chapter 20. In particular, as we shall see, problems with inequality constraints can also be treated using Lagrange multipliers.
We consider the following problem:
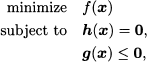
where f : 
n →, h : n → m, m ≤ n, and g: n → p. For the general problem above, we adopt the following definitions.
Definition 21.1 An inequality constraint gj(x) ≤ 0 is said to be active at x* if gj(x*) = 0. It is inactive at x* if gj(x*) < 0.
By convention, we consider an equality constraint hi(x) = 0 to be always active.
Definition 21.2 Let x* satisfy h(x*) = 0, g(x*) ≤ 0, and let J(x*) be the index set of active inequality ...
Get An Introduction to Optimization, 4th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
