Problems
17.1 Let
![]()
and q(x) be the proposal distribution. Show that if
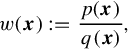
and
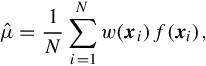
then the variance
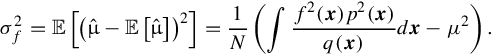
Observe that if f2(x)p2(x) goes to zero slower than q(x), then for fixed N, .
17.2 In importance sampling, with weights defined as
Get Machine Learning now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

