Algorithms in a Nutshell

Convex Hull Scan

To develop an efficient algorithm for computing the convex hull (whose fact sheet appears in Figure 9-7) for a set of points P, we could choose an iterative approach, as shown in Figure 9-8. To determine the next point in the hull, compute the smallest angular difference formed by all non-hull points with an infinite ray determined by the last two discovered hull points. When the partial convex hull contains h points, the angles must be computed for n-h points to determine the next point; this approach is unable to prune away wasted computations that will clearly not be needed.

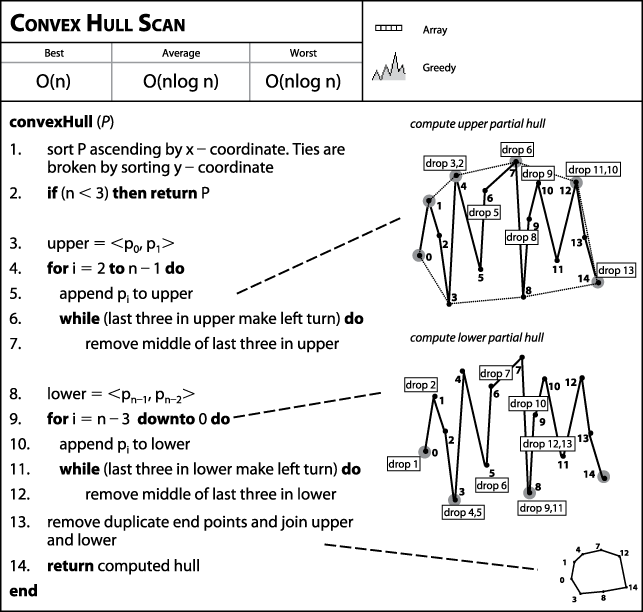
Figure 9-7. Convex Hull Scan fact sheet

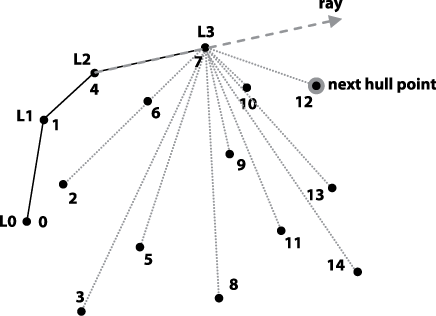
Figure 9-8. Incremental construction of a convex hull

Andrew's Convex Hull Scan divides the problem into two parts—constructing the partial upper hull and the partial lower hull. First, all points are sorted by their x coordinate (breaking ties by considering the y). Note that the points in Figure 9-8 are already numbered from left to right along the x axis. The partial upper hull starts with the leftmost twopoints in P. Convex Hull Scan extends the partial upper hull by finding the point p in P whose x coordinate comes next in sorted order after the partial upper hull's last point L_i.

If the three points L_i−1, L_i and the candidate point p form a right turn, ...