Game Theory: An Introduction, 2nd Edition

Problem Solutions

Solutions for Chapter 1

1.1 Think of this as a 100 × 100 game matrix and we are looking for the upper and lower values except that we are really doing it for the transpose of the matrix.

If we take the maximum in each row and then Javier is the minimum maximum, Javier is v+. If we take the minimum in each column, and Raoul is the maximum of those, then Raoul is the maximum minimum, or v−. Thus, Javier is richer.

Another way to think of this is that the poorest rich guy is wealthier than the richest poor guy. Common sense.

1.3.a The rock-paper-scissors game matrix with the rules of the problem is

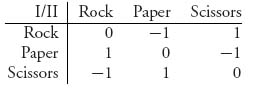
1.3.b v+ = 1, v− = −1. No saddle point in pure strategies since v+ > v−.

1.5 For each player we let (i, j) be the pure strategy in which the player shows i fingers, and guesses the other player will show j fingers. The matrix is

Since v+ = 2, v− = − 2, there are no pure optimal strategies.

1.7 Consider first the game with A. To calculate v− we take the minimum of x and 0, written as { x, 0 }, and the minimum of 1, 2, which is 1. Then

since min { x, 0 } ≤ 0, no matter what x is. Similarly,

Thus, v− = v+ = 1 and there is a pure saddle at row 2, column 1. ...