Algorithms and Parallel Computing

8.7 USEFUL THEOREMS

We show in this section some useful theorems related to the formal technique we proposed in the previous section. The following theorem discusses how we can check if a given algorithm is cycle free or not.

Theorem 8.1

An algorithm with W nodes/tasks is cycle free if and only if A^k has zeros in its main diagonal elements for 1 ≤ k ≤ W.

Proof:

Assume the algorithm is cycle free. In that case, we do not expect any diagonal element to be nonzero for A^k with k ≥ 1. The worst case situation is when our algorithm has all the nodes connected in one long string of W nodes as shown in Fig. 8.5a. The highest power for A^k is when k = W − 1 since this is the maximum length of the path between W nodes. A^W = 0 since there is no path of length W. Thus, a cycle-free algorithm will produce zero diagonal elements for all powers of A^k with 1 ≤ k ≤ W.

Figure 8.5 Worst case algorithm that has 10 nodes. (a) When the algorithm is cycle free. (b) The longest possible cycle in an algorithm with 10 nodes is 10.

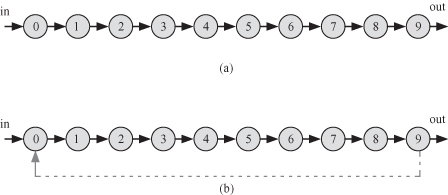
Now assume that all powers of A^k for 1 ≤ k ≤ W are all zero diagonal elements. This proves that we do not have any cycles of length 1 to W in the algorithm. This proves that the algorithm does not have any cycles since for W nodes, we cannot have a cycle of length greater than W. Figure 8.5b shows the longest possible cycle in an algorithm of W nodes/tasks.

The following ...