Algorithms and Parallel Computing

15.7 DESIGN 2: DESIGN SPACE EXPLORATION WHEN s = [1 −1]t

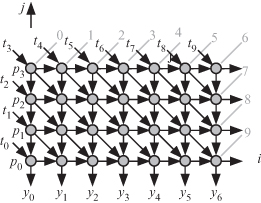
Figure 15.8 shows how the dependence of Fig. 15.1 is transformed to the DAG associated with s = [1 1]^t. The equitemporal planes are shown by the gray lines and the execution order is indicated by the gray numbers. We note that the variables P, T, and Y are pipelined between tasks.

Figure 15.8 DAG for Design 2 when n = 10 and m = 4.

There are three simple projection vectors such that all of them satisfy Eq. 15.12 for the scheduling function. The three projection vectors are

(15.26)

(15.27)

(15.28)

Our multithreading design space now allows for three configurations for each projection vector for the chosen timing function.

15.7.1 Design 2.a: Using s = [1 −1]^t and d_a = [1 0]^t

The resulting is shown in Fig. 15.9 for the case when n = 10 and m = 4. Input T is pipelined between the tasks and task T_i is allocated pattern p_i. The partial results for Y are pipelined such that the outputs are obtained from task T₀.

Figure 15.9 ...