21
Inverse Laplace Transform
Like the operations of addition, multiplication, and differentiation, the Laplace transform has also its inverse. During the process of solving physical problems like differential equations, it is necessary to invoke the inverse transform of the Laplace transform. Thus given a Laplace transform F(s) of a function f, we would like to know what f is. Hence, we are concerned with the solution of the integral equation,
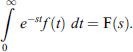
21.1 DEFINITION AND EXAMPLES OF INVERSE LAPLACE TRANSFORM
Definition 21.1. Let f have Laplace transform F(s), that is, L{ f(t)} = F(s), then f(t) is called an inverse Laplace transform of F(s) and ...
Get Engineering Mathematics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

