Feedback Control for Computer Systems

Chapter 22. PID Controllers

We encountered PID controllers already in Chapter 4. Now we take a closer look at them while using the frequency-space methods introduced in Chapter 20.

The Transfer Function of the PID Controller

As we saw in Chapter 4, the output u_PID(t) of a PID controller in terms of its input e(t) is given by

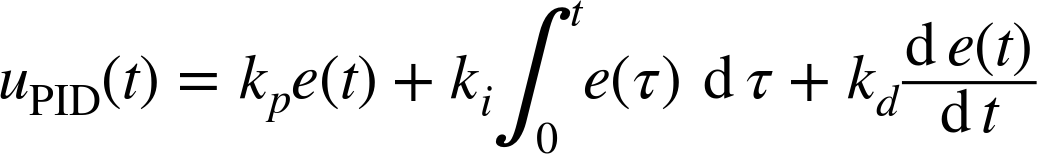
Notice that u_PID(t) is linear in e(t). (Both integration and differentiation are linear operations.) The linearity of the PID controller is one reason for its popularity.

We can take the Laplace transform of this expression term by term to obtain the dynamic response of a PID controller in the frequency domain. Using Table 20-1, we find without difficulty that

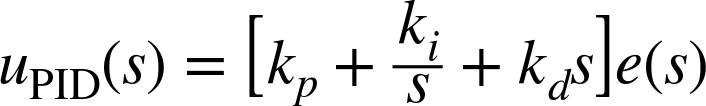
The expression within brackets is the transfer function of the controller in frequency space. It has a particularly simple form—in fact, just the factors s and 1/s are often used to signify the corresponding terms (see Figure 22-1).

Figure 22-1. The standard form of the three-term or PID controller.

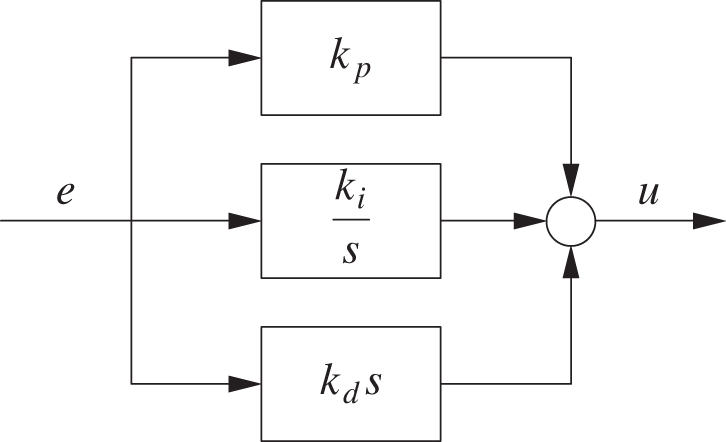
The Canonical Form of the PID Controller

As we have just seen, the transfer function of a PID controller is

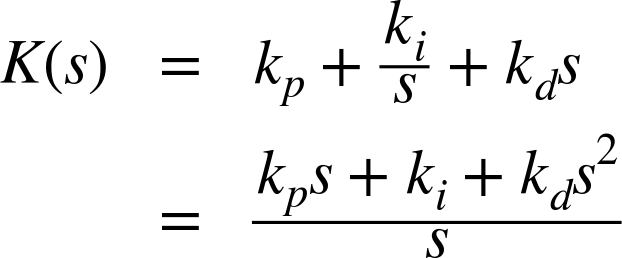
This is the form ...