Java Cryptography

ElGamal

ElGamal is named after its creator, Taher ElGamal. Although it was not patented directly, a patent covering Diffie-Hellman key exchange was considered to cover ElGamal as well. Lucky for us, the patent expired as I wrote this book. ElGamal is now free.

I won’t try to explain the math or demonstrate why it’s a secure set of algorithms. The equations themselves are not too hard to understand.

Key Pair Generation

Here’s the recipe for generating a key pair:

1. Create a random prime number, p. This number is called the modulus. The size of p is the same as the key size, so a 2048-bit key has a p that is 2048 bits.

2. Choose two other random numbers, g and x, both less than p. The private key is x.

3. Calculate y = g^x mod p. The public key is p, g, and y.

Signature

To generate a signature using the private key, follow these steps:

1. Choose a random number, k, that is relatively prime to p - 1. Relatively prime means that k and p - 1 have no factors in common (except 1).

2. Calculate and 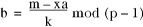, where m is the message. The signature is the numbers a and b.

To verify such a signature, you just have to check that

Cipher

ElGamal encryption consists of two steps:

1. Choose a random number, k, that is relatively prime to ...