Loss Models: From Data to Decisions, 4th Edition

6.5 The (a, b, 0) class

The following definition characterizes the members of this class of distributions.

Definition 6.4 Let p_k be the pf of a discrete random variable. It is a member of the (a, b, 0) class of distributions provided that there exists constants a and b such that

This recursion describes the relative size of successive probabilities in the counting distribution. The probability at zero, p₀, can be obtained from the recursive formula because the probabilities must sum to 1. The (a, b, 0) class of distributions is a two-parameter class, the two parameters being a and b. By substituting in the probability function for each of the Poisson, binomial, and negative binomial distributions on the left-hand side of the recursion, it can be seen that each of these three distributions satisfies the recursion and that the values of a and b are as given in Table 6.1. In addition, the table gives the value of p₀, the starting value for the recursion. The geometric distribution, the one-parameter special case (r = 1) of the negative binomial distribution, is also in the table.

Table 6.1 Members of the (a, b, 0) class.

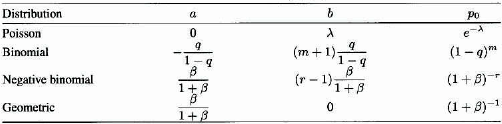
It can be shown (see Panjer and Willmot [89, Chapter 6]) that these are the only possible distributions satisfying this recursive formula.

The recursive formula can ...