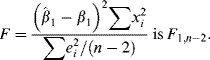Statistical Inference: A Short Course

13.10 Applications of the F Statistic to Regression Analysis

13.10.1 Testing the Significance of the Regression Relationship Between X and Y

We previously used a t test to determine if X contributes significantly to the variation in Y. If H₀: β₁ = 0 is true (we posit “no linear relationship” between X and Y), then the sole source of variation in Y is the random disturbance term ε since the population regression sum of squares is zero. Now, it can be demonstrated that the statistic

(13.28)

Under H₀: β₁ = 0, Equation (13.28) becomes

(13.28.1)

Here the appropriate alternative hypothesis is H₁: β₁ ≠ 0 so that the critical region is (we have a one-tail alternative using the upper tail of the F distribution). So if we reject H₀ in favor of H₁, then we can safely conclude that there exists a statistically significant linear relationship between X and Y at the 100 α% level.

Example 13.10

Using the information provided in Table 12.4, let us conduct a significance test of the linear relationship between X and Y for α = 0.05. Here we test H₀: β₁ = 0, against H₁: β₁ ≠ 0 with . Using Equation (13.28.1) ...