2.3. The inverse z-transform
2.3.1. Introduction
The purpose of this section is to present the methods that help us find the expression of a discrete-time signal from its z-transform. This often presents problems that can be difficult to resolve. Applying the residual theorem often helps to determine the sequence {x(k)}, but the application can be long and cumbersome. So in practice, we tend to use simpler methods, notably those based on development by division, according to increasing the powers in z−1, which constitutes a decomposition of the system into subsystems. Nearly all the z-transforms that we see in filtering are, in effect, rational fractions.
2.3.2. Methods of determining inverse z-transforms
2.3.2.1. Cauchy's theorem: a case of complex variables
If we acknowledge that, in the ROC, the z-transform of {x(k)}, written Xz(z), has a Laurent serial development, we have:
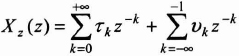
The coefficients τk and νk are the values of the discrete sequence {x(k)} that are to be determined. They can be obtained by calculating the integral ![]() (where C is a closed contour in the interior of the ROC), by the residual method as follows:
(where C is a closed contour in the interior of the ROC), by the residual method as follows:
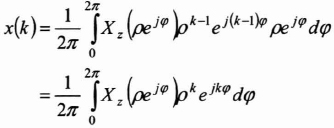
where ρ belongs to the ROC.
DEMONSTRATION 2.8.– let us look at a ...
Get Digital Filters Design for Signal and Image Processing now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

