Digital Filters Design for Signal and Image Processing

2.4. Transfer functions and difference equations

2.4.1. The transfer function of a continuous system

A continuous linear system whose input is x(t) produces a response y(t). This system is regulated by a linear differential equation with constant coefficients that links x(t) and y(t). The most general expression of this differential equation is in the form:

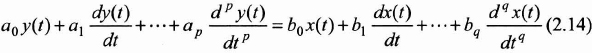
By assuming that x(t) = y(t) = 0 for t < 0, we will show that if we apply the Laplace transform to the differential equation (2.14), we will obtain an explicit relation between the Laplace transforms of x(t) and y(t).

Since:

and:

we get:

The relation of the Laplace transforms of the input and output of the system gives the system transmittance, or even what we can term the transfer function. It equals:

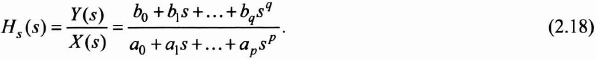
This means that whatever the nature of the input (unit sample sequence, unit step signal, unit ramp signal), we can easily obtain the Laplace transform of the output:

The frequency transform of the output generated by the system can ...