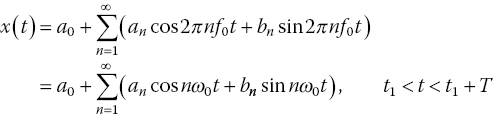12Frequency Content of Digital Signals
12.1 Fourier Series and Frequency Content of Signals
12.1.1 Trigonometric Fourier Series
Any periodic function can be represented as an infinite sum of sinusoids:
An expansion of this type is known as a Fourier Series Expansion (Kreyszig, 1999, p. 530).
Note that each sinusoidal component has a frequency that is a multiple of the fundamental frequency, 
, and the radian fundamental frequency is 
.
There are two forms of the Fourier series: trigonometric and exponential. The form in Eq. (12.1) is called the trigonometric form.
The multiples of the fundamental frequency, f0, are called harmonics of that fundamental frequency. The coefficients a0, an, bn are called the Fourier coefficients.
The Fourier coefficients are determined from the following formulas:
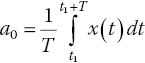
Note that a0 is the average value of x(t) over 
.
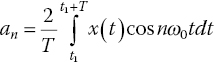
Get Foundations of Electromagnetic Compatibility with Practical Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
