Bayesian Statistics: An Introduction, 4th Edition

5.6 Comparison of two proportions; the $2\times 2$ table

5.6.1 Methods based on the log-odds ratio

In this section, we are concerned with another two sample problem, but this time one arising from the binomial rather than the normal distribution. Suppose

and that we are interested in the relationship between π and ρ. Another way of describing this situation is in terms of a 2 × 2 table (sometimes called a 2 × 2 contingency table)

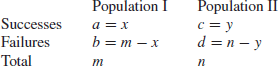
We shall suppose that the priors for π and ρ are such that and , independently of one another. It follows that the posteriors are also beta distributions, and more precisely if

then

We recall from Section 3.1 on the binomial distribution that if

then , so that