Bayesian Statistics: An Introduction, 4th Edition

10.6 Exercises on Chapter 10

1. Show that in importance sampling the choice

minimizes even in cases where f(x) is not of constant sign.

2. Suppose that has a Cauchy distribution. It is easily shown that , but we will consider Monte Carlo methods of evaluating this probability.

a. Show that if k is the number of values taken from a random sample of size n with a Cauchy distribution, then k/n is an estimate with variance 0.125 802 7/n.

b. Let p(x)=2/x2, so that . Show that if is uniformly distributed over the unit interval then y=2/x has the density p(x) and that all values of y satisfy and hence that

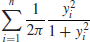
gives an estimate of by importance sampling.

c. Deduce that if are independent U(0, ...