October 2020
Intermediate to advanced
693 pages
16h 26m
Chinese
Content preview from 机器学习实战：基于Scikit-Learn、Keras 和TensorFlow （原书第2 版）
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
Start your free trial
124
｜
第
4
章
不错：模型估算
yx x
ˆ
= ++0.56 0.93 1.78
11
2
，而实际上原始函数为
yx x= + ++0.5 1.0 2.0
11
2
高
斯噪声。
请注意，当存在多个特征时，多项式回归能够找到特征之间的关系（这是普通线性回归模
型无法做到的）。PolynomialFeatures 还可以将特征的所有组合添加到给定的多项式
阶数。例如，如果有两个特征
a
和
b
，则 degree = 3 的 PolynomialFeatures 不仅会
添加特征
a
2
、
a
3
、
b
2
和
b
3
，还会添加组合
ab
、
a
2
b
和
ab
2
。
PolynomialFeatures(degree=d) 可以将一个包含
n
个特征的数组转换
为包含
( )!nd
dn
+
!!
个特征的数组，其中
n
! 是
n
的阶乘，等于 1
×
2
×
3
×
…
×
n
。
要小心特征组合的数量爆炸。
4.4 学习曲线
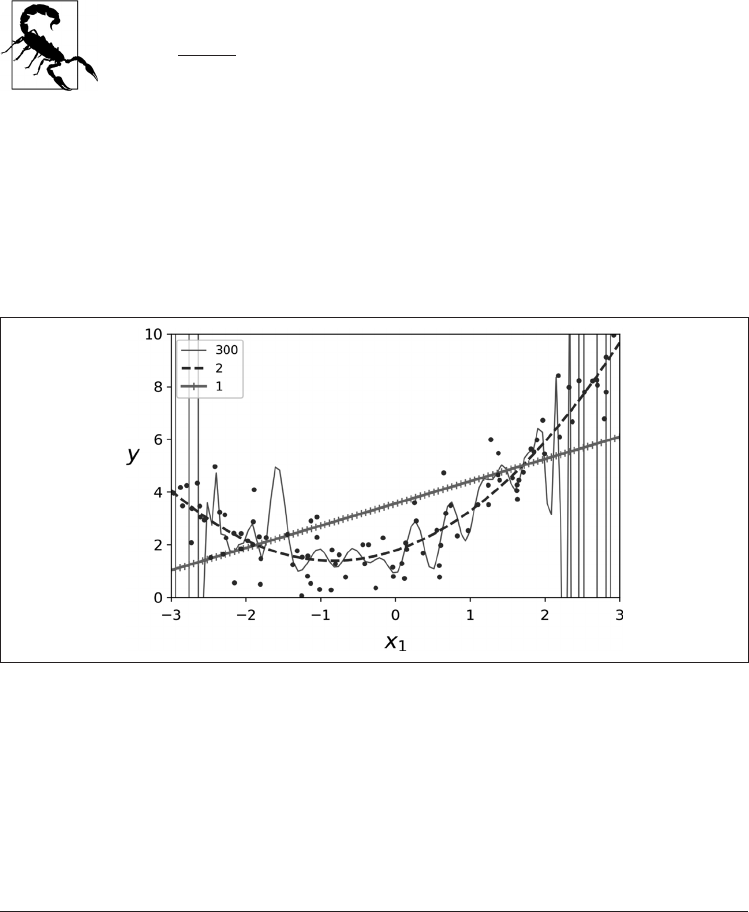
你如果执行高阶多项式回归，与普通线性回归相比，拟合数据可能会更好。例如，图 4-14
将 300 阶多项式模型应用于先前的训练数据，将结果与纯线性模型和二次模型（二次多
项式）进行比较。请注意 300 阶多项式模型是如何摆动以尽可能接近训练实例的。
图 4-14：高阶多项式回归
这种高阶多项式回归模型严重过拟合训练数据，而线性模型则欠拟合。在这种情况下，
最能泛化的模型是二次模型，因为数据是使用二次模型生成的。但是总的来说，你不知
道数据由什么函数生成，那么如何确定模型的复杂性呢？你如何判断模型是过拟合数据
还是欠拟合数据呢？
在第 2 章中，你使用交叉验证来估计模型的泛化性能 ...