机器学习实战：基于Scikit-Learn、Keras 和TensorFlow （原书第2 版）

194

｜

第

8

章

8.1 维度的诅咒

我们太习惯三维空间

注 1

的生活，所以当我们试图去想象一个高维空间时，直觉思维很难

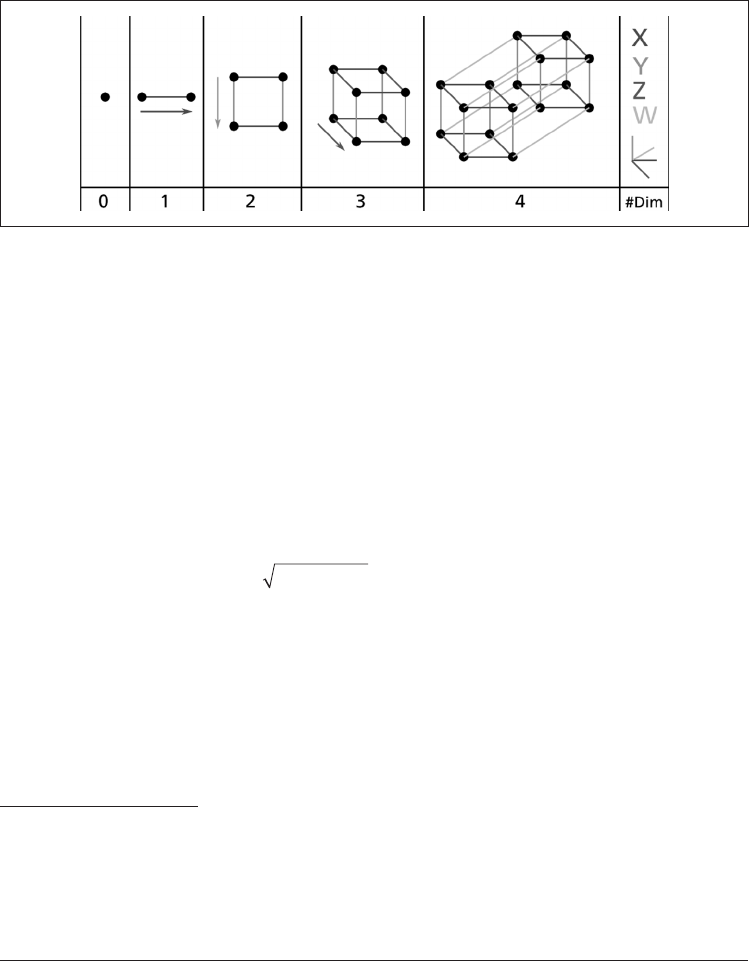
成功。即使是一个基本的四维超立方体（见图 8-1），我们也很难在脑海中想象出来，更

不用说在一个千维空间中弯曲的二百维椭圆体。

图 8-1：点、线段、正方形、立方体和网格（零维至四维超立方体）

注 2

事实证明，在高维空间中，许多事物的行为都迥然不同。例如，如果你在一个单位平

面（1

×

1 的正方形）内随机选择一个点，那么这个点离边界的距离小于 0.001 的概率

只有约 0.4%（也就是说，一个随机的点不大可能刚好位于某个维度的“极端”）。但是，

在一个 10 000 维的单位超立方体（1

×

1…

×

1 立方体，一万个 1 ）中，这个概率大于

99.99999%。高维超立方体中大多数点都非常接近边界

注 3

。

还有一个更麻烦的区别：如果你在单位平面中随机挑两个点，这两个点之间的平均距离

大约为 0.52。如果在三维的单位立方体中随机挑两个点，两点之间的平均距离大约为

0.66。但是，如果在一个 100 万维的超立方体中随机挑两个点呢？不管你相信与否，平

均距离大约为 408.25（约等于

1000 000 / 6

）！这是非常违背直觉的：位于同一个单位

超立方体中的两个点，怎么可能距离如此之远？这个事实说明高维数据集有很大可能是

非常稀疏的：大多数训练实例可能彼此之间相距很远。当然，这也意味着新的实例很可

能远离任何一个训练实例，导致跟低维度相比，预测更加不可靠，因为它们基于更大的

推测。简而言之，训练集的维度越高，过拟合的风险就越大。 ...