机器学习实战：基于Scikit-Learn、Keras 和TensorFlow （原书第2 版）

支持向量机

｜

151

和

O

(

m

3

×

n

) 之间。很不幸，这意味着如果训练实例的数量变大（例如成千上万的实例），

它将会慢得可怕，所以这个算法完美适用于复杂但是中小型的训练集。但是，它还是

可以良好地适应特征数量的增加，特别是应对稀疏特征（即每个实例仅有少量的非零特

征）。在这种情况下，算法复杂度大致与实例的平均非零特征数成比例。表 5-1 比较了

Scikit-Learn 的 SVM 分类器类。

表 5-1：用于 SVM 分类的 Scikit-Learn 类的比较

类 时间复杂度 核外支持 　　需要缩放 核技巧

LinearSVC

O

(

m

×

n

) 否 　　是 否

SGDClassifier

O

(

m

×

n

) 是 　　是 否

SVC

O

(

m

2

×

n

) 到

O

(

m

3

×

n

) 否 　　是 是

5.3 SVM 回归

正如前面提到的，SVM 算法非常全面：它不仅支持线性和非线性分类，而且还支持线性

和非线性回归。诀窍在于将目标反转一下：不再尝试拟合两个类之间可能的最宽街道的同

时限制间隔违例，SVM 回归要做的是让尽可能多的实例位于街道上，同时限制间隔违例

（也就是不在街道上的实例）。街道的宽度由超参数

ε

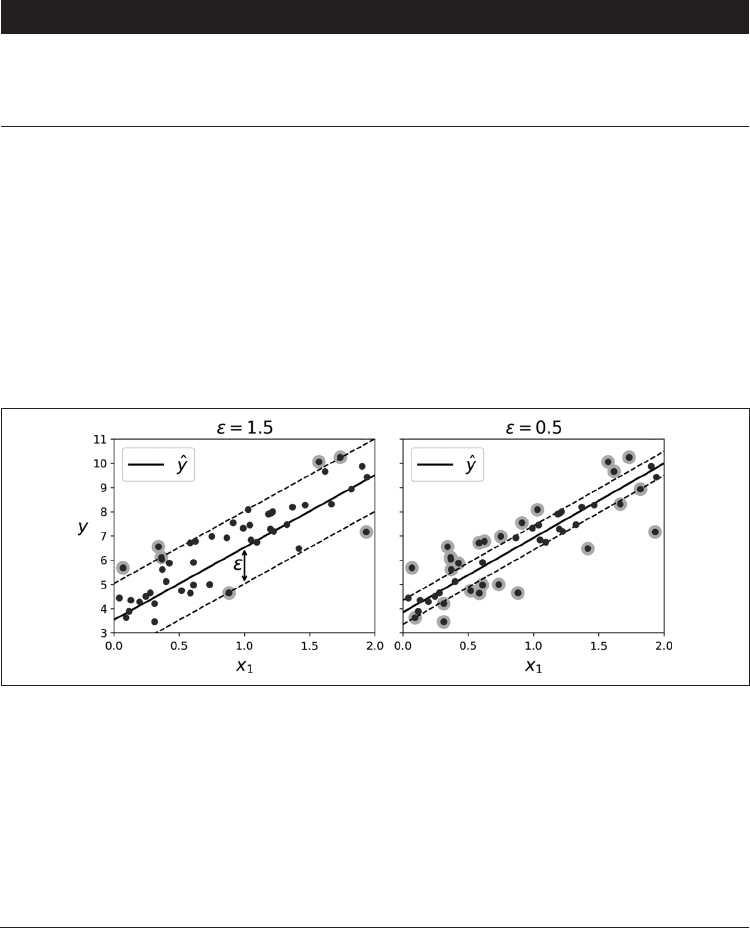
控制。图 5-10 显示了用随机线性数

据训练的两个线性 SVM 回归模型，一个间隔较大（

ε

= 1.5），另一个间隔较小（

ε

= 0.5）。

图 5-10：SVM 回归

在间隔内添加更多的实例不会影响模型的预测，所以这个模型被称为

ε

不敏感。

你可以使用 Scikit-Learn 的 LinearSVR ...