机器学习实战：基于Scikit-Learn、Keras 和TensorFlow （原书第2 版）

170

｜

第

6

章

CART 算法的工作原理与以前的方法大致相同，不同之处在于，它不再尝试以最小化不

纯度的方式来拆分训练集，而是以最小化 MSE 的方式来拆分训练集。公式 6-4 给出了算

法试图最小化的成本函数。

公式 6-4：CART 回归成本函数

其中

Jkt( , ) MSE MSE















k

MSE ( )

y

ˆ

node

= +

m

mm

=

node node

left

i∈

∑

=

node

m

i∈

node

∑

node

y

()

left right

i

yy

ˆ

m

right

−

() 2i

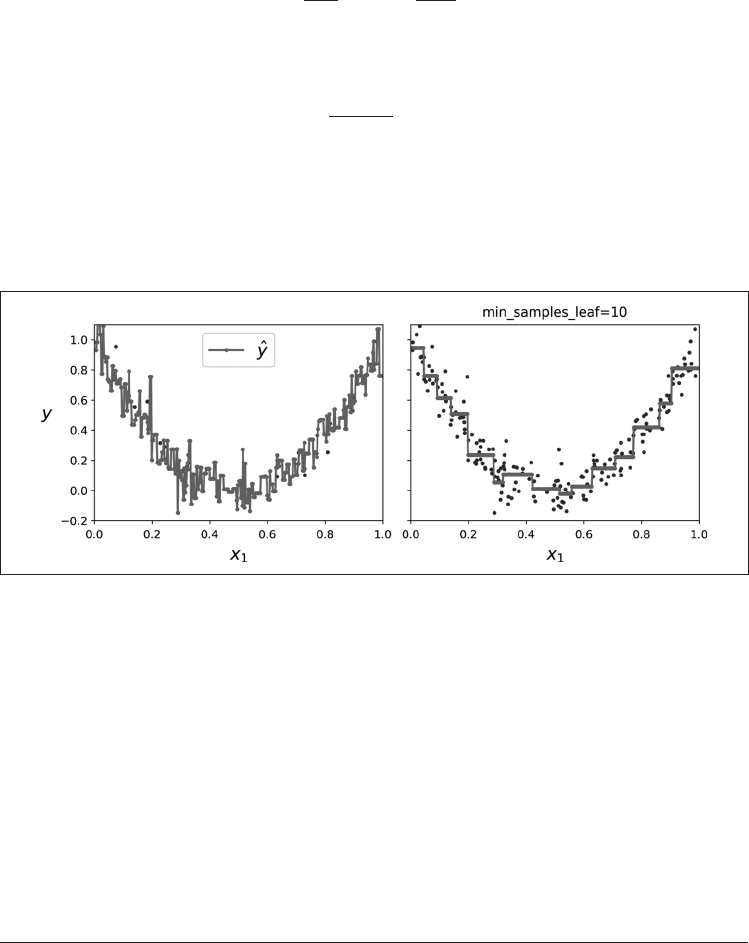
就像分类任务一样，决策树在处理回归任务时容易过拟合。如果不进行任何正则化（如

使用默认的超参数），你会得到图 6-6 左侧的预测。这些预测显然非常过拟合训练集。只

需设置 min_samples_leaf = 10 就可以得到一个更合理的模型，如图 6-6 右侧所示。

没有限制

图 6-6：正则化一个回归决策树

6.9 不稳定性

希望到目前为止，你已经确信决策树有很多用处：它们易于理解和解释、易于使用、用

途广泛且功能强大。但是，它们确实有一些局限性。首先，你可能已经注意到，决策树喜

欢正交的决策边界（所有分割都垂直于轴），这使它们对训练集旋转敏感。例如，图 6-7

显示了一个简单的线性可分离数据集：在左侧，决策树可以轻松地对其进行拆分，而在

右侧，将数据集旋转 45 度后，决策边界看起来复杂了（没有必要）。尽管两个决策树都

非常拟合训练集，但右侧的模型可能无法很好地泛化。限制此问题的一种方法是使用主

成分分析（见第 8 章），这通常会使训练数据的方向更好。 ...