Fundamentals of Photonics, 2 Volume Set, 3rd Edition

APPENDIX A FOURIER TRANSFORM

This appendix provides a brief review of the Fourier transform, and its properties, for functions of one and two variables.

A.1 ONE-DIMENSIONAL FOURIER TRANSFORM

The harmonic function F exp(j2πνt) plays an important role in science and engineering. It has frequency ν and complex amplitude F. Its real part |F| cos(2πνt + arg{F }) is a cosine function with amplitude |F| and phase arg{F }. The variable t usually represents time; the frequency ν has units of cycles/s or Hz. The harmonic function is regarded as a building block from which other functions may be obtained by a simple superposition.

In accordance with the Fourier theorem, a complex-valued function f (t), satisfying some rather unrestrictive conditions, may be decomposed as a superposition integral of harmonic functions of different frequencies and complex amplitudes,

(A.1-1) Inverse Fourier Transform

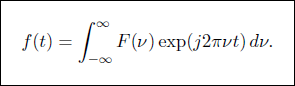
The component with frequency ν has a complex amplitude F (ν) given by

(A.1-2) Fourier Transform

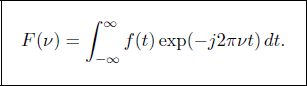
F(ν) is termed the Fourier transform of f(t), and f(t) is the inverse Fourier transform of F(ν). The functions f(t) and F(ν) form a Fourier transform pair; if one is known, the other may be determined.

In this book we adopt the convention that exp(j2πνt) is a harmonic function with positive frequency, ...