Learning Functional Programming in Go

Function composition

Function composition is what happens when we combine functions. The output of one function is the the input of the next function. We can use objects and morphisms of category theory to help us get the order right. Take the following diagram for example...

>

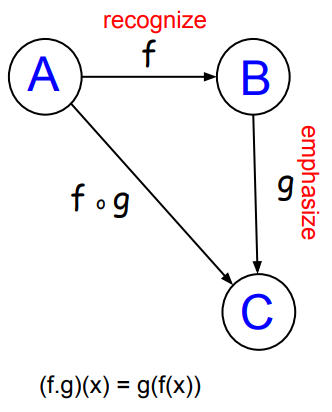We see that we can combine our functions f and g to get from A to B to C. Note that the order matters. We must first go from A to B via f and then from B to C via g.  

We express this with the following notation (f.g)(x). That reads, f-compose-g with input x. This expression equals g(f(x)), which reads f of x of g. So (f.g)(x) == g(f(x)).

This is what the compose function ...