3.4 PROBABILITY MASS FUNCTION
An example of the distribution function for a discrete random variable is shown in Figure 3.8. Observe that there are two distinguishing features of this type of distribution function:
FIGURE 3.8 Distribution function for a discrete (Bernoulli) random variable.
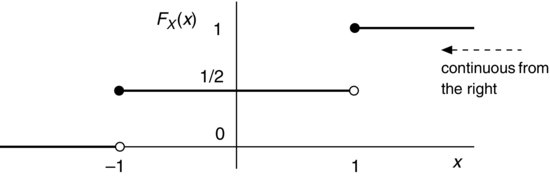
- FX(x) changes instantaneously at values of x that are outcomes of the random variable.
- FX(x) remains constant between these outcomes.
There are two useful ways of representing the outcomes and the probability assignment for a discrete random variable, using either the Kronecker delta function or the Dirac delta function 
. The distribution function in Figure 3.8 corresponds to the symmetric Bernoulli random variable with equally likely outcomes 
. This random variable would arise, for example, when tossing a single fair coin with the mapping: 
and 
.
The Kronecker delta function is convenient for representing the outcomes of a discrete random variable because there are no continuity issues. Moreover, ...
Get Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
