November 2012
Intermediate to advanced
794 pages
22h 9m
English
book
Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications
by John J. Shynk
Content preview from Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
7.7 DIFFERENTIAL EQUATIONS
Many systems in engineering are modeled by linear DEs with constant coefficients to describe how various quantities (signals, voltages, currents, and so on) change with time. For convenience in our discussion, we provide a simple example for a second-order RLC circuit.
FIGURE 7.17 Parallel RLC circuit. Current source is is switched on at t = 0 as indicated by the unit step-function u(t).
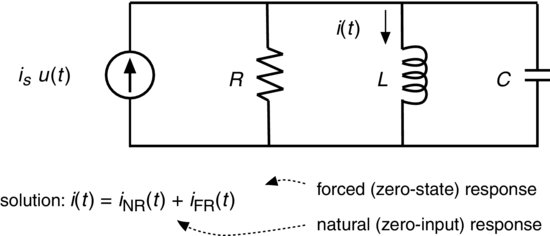
Example 7.22. A parallel RLC circuit (with resistor R, inductor L, and capacitor C) has an independent current source is that is switched on at time t = 0. The current through the inductor can be modeled by the following second-order DE:
where the coefficients {a0, a1, a2} are functions of {R, L, C} and u(t) is the unit-step function. A circuit diagram is provided in Figure 7.17 for which it can be shown
(7.157) 
Depending on the coefficient values, the solution of (7.156) can take on one of three forms:
(7.159) 
(7.160)
where and are functions of { ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.