A lot of real-world phenomena can be called dynamical systems. The state of such systems varies with time. Modeling such systems requires the use of differential equations. We will take here an example of modeling a pendulum attached to a spring, as shown in the following image. The pendulum swings to and fro. Furthermore, since the bob is attached to a spring, the bob also oscillates up and down:
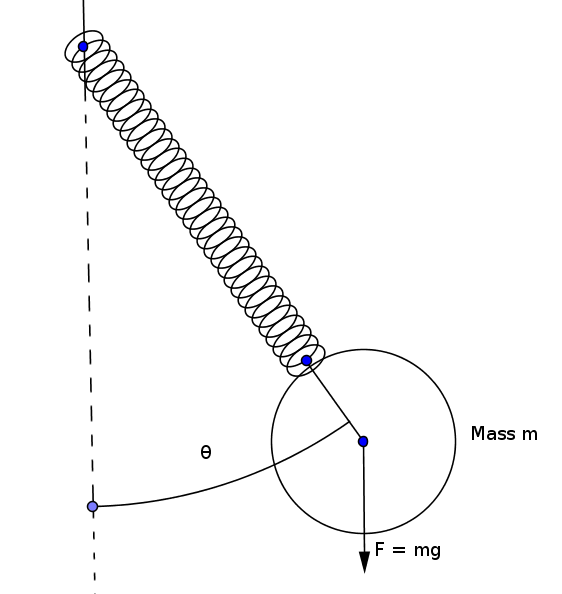
We study the evolution of two variables over time:
- Length l of the spring
- Angle (θ) between the spring and the center line, as shown in the preceding diagram.
Since there are two variables changing over time, the state ...

