Problem 5
Huygens and the Gambler's Ruin (1657)
Problem. Two players A and B, having initial amounts of money a and (t − a) dollars, respectively, play a game in which the probability that A wins a round is p and the probability that B wins is q = 1 − p. Each time A wins, he gets one dollar from B, otherwise he gives B one dollar. What is the probability that A will eventually get all of B's money?
Solution. Let 
be the probability that A eventually wins all the t dollars (i.e., ruins B), starting with a dollars. Then, conditioning on the first round, we can obtain the following difference equation for 
:
with 
To solve the above difference equation, we let 
, where 
is a constant. Therefore, Eq. (5.1) becomes
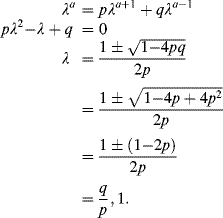
In the case , we have two distinct roots so that , where C and D are arbitrary ...
