Problem 19
Bertrand's Chords (1889)
Problem. A chord is randomly chosen on a circle. Calculate the probability that the chord is longer than the side of an equilateral triangle inscribed inside the circle.
Solution. There are at least three methods a chord can be randomly chosen on the circle, as shown in Fig. 19.1.
Figure 19.1 Three of the ways in which a chord can be randomly chosen on a circle.
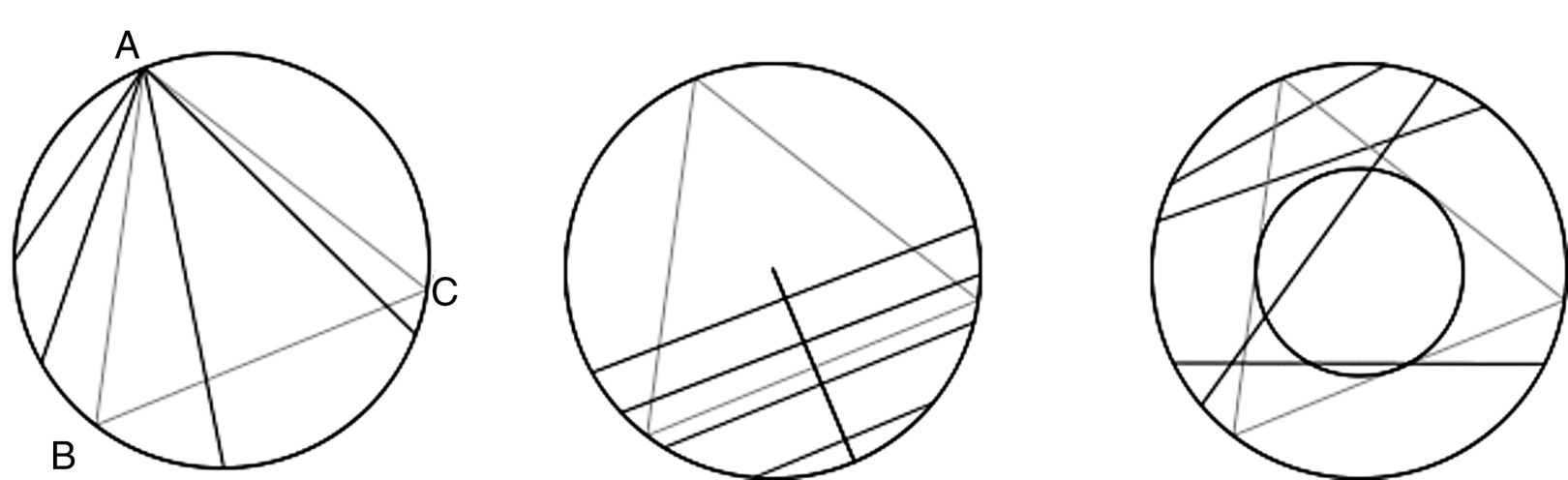
Solution 1: Random Endpoints Approach. Consider the first figure. We randomly choose two endpoints on the circumference of the circle and join them to obtain the chord. Because of symmetry, we assume one of the points coincides with one of the vertices of the inscribed triangle (at A). The remaining two vertices (B and C) of the triangle then divide the circumference of the circle into three equal arcs (AC, CB, and BA). The chord is longer than the side of the triangle if and only if it intersects the triangle. The required probability is thus 1/3.
Solution 2: Random Radius Approach. Consider the second figure. We randomly choose a radius of the circle and then select a point on it. The chord is obtained by drawing a perpendicular to the radius across the point. Because of symmetry, we assume the radius is perpendicular to one of the edges of the triangle. The chord is longer than the side of the triangle if and only if the selected point lies on the half of the radius that is closer ...

