Classic Problems of Probability

Problem 32

Monty Hall, Cars, and Goats (1975)

Problem. In a TV prize-game, there are three doors (X, Y, and Z). One of them conceals a car while the other two doors hide a goat each. A contestant chooses one of the doors, say X. The game host knows which door hides the car and opens a door, say Y, which has a goat behind it. The host then gives the contestant the options of either sticking to her original choice (i.e., X) or of switching to the other unopened door (i.e., Z). Which is the better option?

Solution. Let C_X, C_Y, and C_Z be the events that, respectively, doors X, Y, and Z hide the car. Let H_Y be the event that the host opens door Y. Now, since the question assumes the contestant initially chooses door X and the host opens door Y, switching will be a winning strategy only if the car is behind door Z. That is, the probability of winning the car if the contestant switches is , where by Bayes' Theorem¹

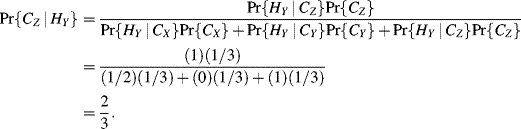
In the above calculation, we have assumed that, when the host has two possible doors to open (i.e., if the car was behind door X), she is equally likely to open any one of them. Further, since the host does not open the door that hides the car, we have , so that

The probability ...