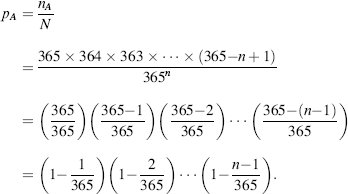Classic Problems of Probability

Problem 28

Coinciding Birthdays (1939)

Problem. What is the least number of people that must be in a room before the probability that some share a birthday becomes at least 50%? Assume there are 365 days each year and that births are equally likely to occur on any day.

Solution. Suppose there are n persons in the room. Then each person can have 365 possible birthdays, so that the total number of possible birthdays for the n individuals is . Let A be the event “each of the n persons has a different birthday.” Then a given person has 365 possibilities for a birthday, the next person has 364 possibilities, and so on. Therefore, the total number of ways the event A can be realized is

Using the classical definition, the probability that all n individuals have a different birthday is

(28.1)

Taking natural logarithms on both sides, we have¹

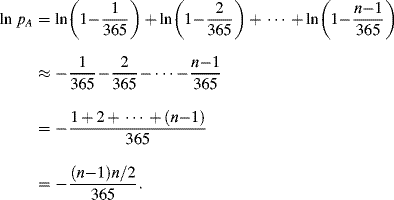
Thus, and the probability that at least two individuals share a birthday is

(28.2)

We now solve obtaining . Since we have used the approximate formula ...