Fibonacci and Catalan Numbers: An Introduction

Chapter 10

Solving Linear Recurrence Relations: The Binet Form for F_n

Up to this point, if we wanted to know a specific Fibonacci number—for instance, F₃₇—we had to start with F₀ = 0, F₁ = 1, and use the recurrence relation F_n = F_n−1 + F_n−2, n ≥ 2, to compute

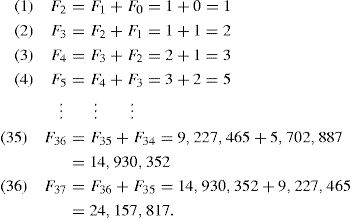
Now our objective is to somehow determine F₃₇, but without performing any of these 36 calculations. To do so, we want to derive an explicit formula for the general term F_n in terms of n—not in terms of previous values in the sequence of Fibonacci numbers. We shall accomplish this by introducing the following idea:

Definition 10.1: For real constants C₀, C₁, C₂, . . ., C_k, with C₀ ≠ 0 and C_k ≠ 0, an expression of the form

where n ≥ k, is called a kth-order linear homogeneous recurrence relation with 53 constant coefficients. When the right side of this recurrence relation is not 0, then the relation is referred to as nonhomogeneous.

We shall focus our concern on the case where k = 2, C₀ = 1, and C₂ ≠ 0. For example,

or

is a second-order linear homogeneous recurrence relation with constant coefficients.

To solve such a recurrence ...