Chapter 31
Rooted Ordered Binary Trees, Pattern Avoidance, and Data Structures
In this chapter we have the opportunity to examine some additional examples where the Catalan numbers arise. This time, however, we shall verify that the structures are counted by these numbers by using the nonlinear recurrence relation developed in Chapter 29.
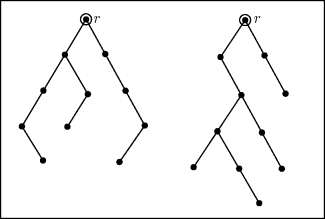
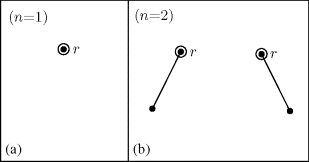
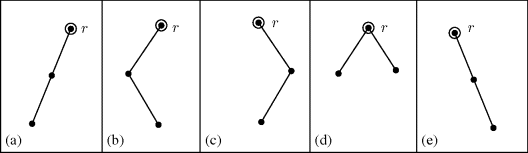
Example 31.1: Consider the trees shown in Fig. 31.1, where the vertices labeled with r are the roots. These trees are called binary because each vertex has at most two edges descending from it. Furthermore, these trees are ordered in the sense that a left branch descending from a vertex is considered to be different from a right branch descending from that vertex. In Fig. 31.2(a) we see the one rooted ordered binary tree for when we have n = 1 vertex—namely, just the root. Part (b) of Fig. 31.2 provides the two trees of this type for n = 2 vertices. If we let tn count the number of rooted ordered binary trees on n vertices, then at this point we have t1 = 1 and t2 = 2. The results in Fig. 31.3 on p. 240 show us that t3 = 5.
To count the number tn of rooted ordered binary trees on n ≥ 0 vertices, we shall assume ...