Chapter 33
The Narayana Numbers
In Example 5.6(a), we learned how each Fibonacci number can be expressed as a sum of binomial coefficients. A somewhat similar situation arises for the Catalan numbers by way of the Narayana numbers. Named after the Indian mathematician Tadepalli Venkata Narayana, the Narayana numbers are defined as follows:
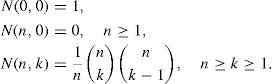
Table 33.1 provides the values of N(n, k) for 1 ≤ k ≤ n ≤ 7.

The last column of Table 33.1 suggests that for n ≥ 1,
![]()
We shall prove that this is indeed the case! Before we do so, however, we would like to know if the individual summands—namely, N(n, k)—have any combinatorial significance. The answer is a resounding “Yes!” The following will provide interpretations of the Narayana numbers for some of the examples we have encountered for the Catalan numbers.
Example 33.1:
1. In Fig. 33.1, we have the five lattice paths from (0, 0) to (3, 3) that never rise above the line y = x. We first encountered these paths in Fig. 19.2 of Example 19.1. Here we see that there is 1 = N(3, 1) such path with one turn—where there is an R followed by a U. Also, there are 3 = N(3, 2) paths with two such turns, and 1 = N(3, 3) path with three such turns. ...

