Chapter 17
One Final Example?
Why the question mark at the end of this chapter title. Is it a misprint? Let us see.
At this point, we want to make sure that the reader understands and appreciates the pains we have gone through in always setting up the somewhat repetitious recurrence relation that arose in the examples where the solution was Fn (or Fn−1, Fn+1, Fn+2, F2n, or F2n+1). When we are proving a theorem, we cannot draw any general conclusions from a few (or even, perhaps, many) particular instances where the result stated in the theorem happens to be true. The same is true here, and the following example should serve to drive this point home!
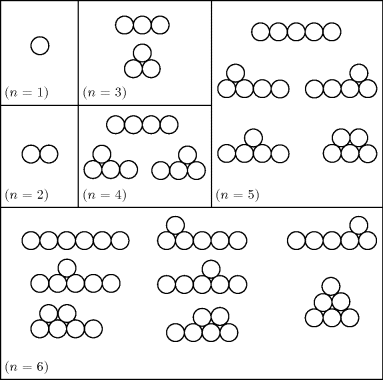
17. We start with n identical circles and let an count the number of ways we can arrange these circles—contiguous in each row—with each circle above the bottom row tangent to two circles in the row below it. In Fig. 17.1, we see the possible ways to so arrange the n circles for 1 ≤ n ≤ 6. It follows from this that
![]()
These results definitely suggest that we have encountered another instance where the Fibonacci numbers arise. But before we write an = Fn, for all n ≥ 1, remember that we have not presented a general argument or set up a recurrence relation.
Unfortunately, we have been led astray in this instance. Here one finds, ...