Chapter 15
The gcd Property for the Fibonacci Numbers
First and foremost, the reader may be puzzling over what we mean by the gcd Property. Instead of simply stating it, as if it comes out of nowhere, let us present some motivation for this amazing property. So consider the following two examples:
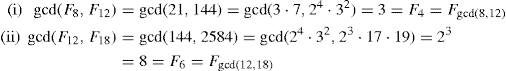
These results suggest the following:
Property 15.1: For m ≥ n ≥ 1,
To establish this property, we return to the matrix Q of Chapter 14.
For m, n ≥ 1, we know that Qm+n = QmQn. Previously we learned from Theorem 14.1 that 
for k ≥ 1. So Qm+n = QmQn now becomes
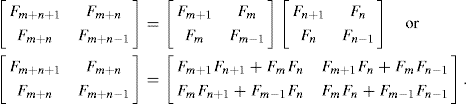
When two matrices are equal, their corresponding entries must be equal. Consequently, we arrive at the following four results. For m, n ≥ 1,
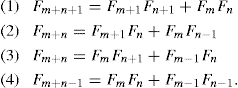
Result (3) is precisely Property 7.1 of Example 7.3, which we established by a combinatorial argument involving the tiling of a 1 × (n + m − 1) chessboard. Results (1), (2), and (4) are simply variations of Property 7.1. The matrix Q has now provided another way to obtain Property 7.1, as well as ...
