Chapter 21
Dyck Paths, Peaks, and Valleys
This chapter will provide us with examples that modify and extend what we learned about lattice paths in Chapter 19.
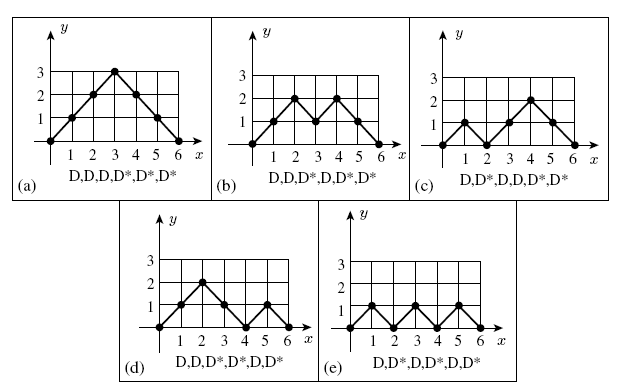
Example 21.1: Let us start by returning to the lattice paths in Example 19.1. This time, however, we shall introduce the following diagonal steps. Replace each
![]()
and each
![]()
The resulting paths in Fig. 21.1 are called Dyck (pronounced “Dike”) paths, after the German mathematician Walther Franz Anton von Dyck (1856–1934). In general, for n ≥ 0, there are Cn Dyck paths of length 2n, made up of n D's and n D*'s. When these paths start at (0, 0) and end at (2n, 0), they never fall below the x-axis. Considering their shape, one also finds the configurations in Fig. 21.1 referred to as mountain ranges.
Example 21.2: Figure 21.2 provides us with what are called the left factors of the Dyck paths in Fig. 21.1. As seen in the figure, the left factor of each Dyck path is made up of all the diagonal steps that precede the last D step. Consequently, each left factor is seen to have the same 171 number of diagonal steps D—namely, 2(= 3 − 1) . We shall establish a one-to-one correspondence between these left factors with n − 1 diagonal ...