Coherent Interactions with Two-Level Systems 239
Absorption
(a) (b)
Refractive index
z
zct
z(c/n) t
t
E
w
l
w
o
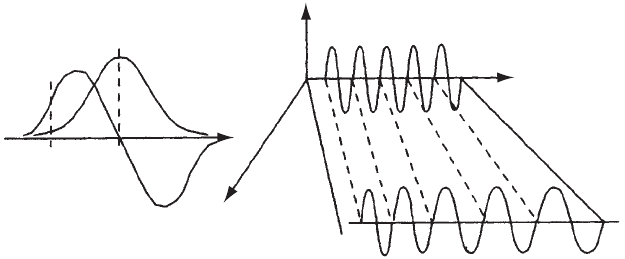
Figure 4.6 Sketch illustrating the evolution of the average frequency of a short pulse as it prop-
agates through matter. Figure (a) shows the relative frequencies of the radiation (ω
) and material
resonance (ω
0
). These are however steady-state values. Prior to applying the field (and for the first
optical cycle(s) of the radiation), the electric dipoles have not yet been induced, and the abscissa
is the correct representation of both the absorption and dispersion. If a square pulse is applied, the
value of the absorption and dispersion evolve with time from the initial condition (0) to the value
on the corresponding curve at ω
. A representation of the evolution of the wave packet in time and
space is shown in (b). The leading edge of the square pulse is not affected, because the dipoles have
not yet been induced. The time varying index leads to a shift of the average pulse frequency to lower
frequencies.
the framework of the SVEA. Numerical simulations indicate that the material
response is larger below resonance than above, leading to a larger red shift than
blue shift. This may not come as a surprise, because the response of a system
with a resonance at ω
0
will “follow” a low frequency (ω
ω
0
) excitation, but
has zero response at frequencies far beyond its resonance (ω
ω
0
).
4.2.4. Steady-State Pulses
A steady-state pulse is a pulse for which the envelope E(t −z/ν
e
) is conserved
along propagation. The quantity ν
e
is the velocity of the pulse envelope. Usually it
depends on properties of the medium and the pulse and differs from the group and
phase velocity. If the pulse envelope remains constant, various pulse parameters
such as the pulse duration, energy, and area should also be conserved.
In the case of inhomogeneously broadened media, the area theorem applies.
From Eq. (4.24), a necessary condition for the existence of a steady-state pulse
is that dθ/dz = (α
0
/2)sin θ
0
= 0. Obviously there are several values of the
area which do not change with distance; they are θ
0
= 0, π,2π,3π, … . A quick
glance at the graphical representation (Fig. 4.3) of Eq. (4.24) indicates that in
an absorbing medium (α<0) the areas θ
0
= 0, 2π,4π… are stable solutions,
240 Coherent Phenomena
although for amplifying media, the stable areas correspond to uneven numbers
of π. At resonance, steady-state pulses correspond to the π pulse. As men-
tioned previously, in the case of an absorber, only the area 2π corresponds to
a stable stationary pulse. In the amplifier, however, even with constant area,
the pulse energy will tend to grow to infinity unless balanced by a loss mecha-
nism. We will use a scattering coefficient σ
s
to describe such a loss mechanism
in searching for steady-state pulses in amplifiers. It is the same coefficient rep-
resenting linear losses as the κ
1
introduced in Eq. (1.142)—the notation σ
s
is
chosen here to avoid confusion with the Rabi coefficient κ.
Transverse effects have been neglected in the search for steady-state solutions
and in the evolution equations derived in the previous sections. In free space,
the plane wave approximation will only hold within the confocal parameter of a
beam of finite size. Even within this limit, transverse effects in coherent interac-
tion may contribute to self-focusing and defocusing of the beam [14]. As a rule of
thumb, the plane wave approximation for self-induced transparency may be
considered to hold for approximately five linear absorption lengths. There are
however two important types of confinements for which the single dimensional
approach remains valid over long distances:
• optical fibers and
• optical cavities.
The search for steady-state solutions in conditions of coherent interactions has
more than purely academic interest. The main motivations for these studies
relate to
• stability,
• minimizing energy losses, and
• maximizing energy extraction.
We have seen in the previous section that the 2π pulse in absorbing media
acts as a filter, “cleaning” the signal from amplitude and phase fluctuations.
The steady-state pulse in an absorber has minimum energy loss, because it returns
the absorbing two-level system to the ground state. In an amplifier or in a laser,
steady-state pulses can be found that bring the two-level system from inversion
to the ground state—and hence extract the maximum energy possible from the
gain medium.
Steady-State Pulses in Amplifiers
For finite T
2
, stable steady-state pulses do not exist in absorbing media.
The loss of coherence leads to irreversible energy losses, causing to the collapse
Get Ultrashort Laser Pulse Phenomena, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

