Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach

CHAPTER 3

EXTENSION OF MEASURES

As defined in the previous chapter, a measure is a set function on an algebra. To extend a measure from an algebra to a σ-algebra, we need some tools. In this chapter, we will introduce concepts and theorems related to measure extension.

3.1 Basic Concepts and Facts

Definition 3.1 (Outer Measure). An outer measure on a set is a nonnegative, extended real-valued set function that satisfies the following conditions:

(a) = 0.

(b) (Monotonicity) If A ⊆ B ⊆ S, then μ*(A) ≤ μ* (B).

(c) (Countable subadditivity) If A_n ⊆ S for all n ≥ 1, then

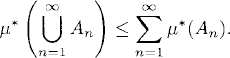
Definition 3.2 (Complete Measure). Let μ be a measure on a σ-algebra ∑. The measure μ, is said to be complete if and only if all subsets of a zero measure set in ∑ are in ∑. Thus, whenever A ∑ with μ(A) = 0, we have B ∑ for all B ⊆ A.

Definition 3.3 (Completion of Measure Spaces). Let (S, ∑, μ) be a measure space. The completion ...