CHAPTER 39
DIFFUSION
A diffusion or a diffusion process is a solution to a stochastic differential equation. In this chapter, we will present some results about diffusion, in particular, Itô diffusion.
39.1 Basic Concepts and Facts
Definition 39.1 (Compact Set). A set K ⊆ R is called a compact set if every open cover of K contains a finite subcover; that is, if {Vi}i![]() I is a collection of open sets such that
I is a collection of open sets such that
![]()
then there exists a finite subcollection {Vij}j=1,2,…,n such that
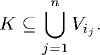
Definition 39.2 (Closure). Let E ⊆ R. The closure of the set E, written as ![]() , is the smallest closed set in R that contains E.
, is the smallest closed set in R that contains E.
Definition 39.3 (Support). The support of a function f on R is the closure of the set
![]()
Definition 39.4 (C1,2-Function). A function f on R × R is called a C1,2-function if f(t, x) is continuously differentiable on t (i.e., ![]() is continuous) and twice continuously differentiable on x (i.e., is continuous). ...
is continuous) and twice continuously differentiable on x (i.e., is continuous). ...
Get Measure, Probability, and Mathematical Finance: A Problem-Oriented Approach now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

